1
Introdução
Para
o dimensionamento de lajes em concreto armado, é bastante comum a utilização de
métodos numéricos, como o Método dos Elementos Finitos (MEF) e Método das Grelhas.
Identificar e escolher qual método utilizar, considerando a segurança
necessária para o empreendimento, aspectos econômicos e a avaliação estrutural,
são desafios para Engenharia Estrutural e Construção Civil. A comparação entre os
diferentes recursos pode indicar suas melhores aplicações e identificar suas
vantagens e desafios. A utilização desses mecanismos em programas
computacionais, com recursos e matrizes numéricas cada vez mais avançada, tem
se tornado tendência e vem sendo bastante utilizado entre engenheiros, mesmo
que esses não tenham experiência para uma avaliação completa dos resultados
diferentes proporcionados pelos vários métodos para uma mesma estrutura.
Dependendo
do software, as diferentes metodologias de cálculo apresentam resultados
que se diferem, não havendo consenso de qual a melhor maneira de se modelar a
estrutura. Poucos têm a oportunidade de trabalhar com profissionais
experientes, e poucos são os profissionais que avaliam diferentes métodos de
dimensionamento em seus projetos, tomando uma decisão embasada acerca da
estrutura que tem seu comportamento mais bem representado. Assim, estudos que
subsidiem análise de diferentes formas de cálculo para dimensionamento
estrutural e avaliação dos resultados são importantes.
Assim, o
presente artigo busca comparar a utilização do método das grelhas e MEF, os
quais são utilizados respectivamente nos softwares: Eberick V8® e
SAP2000 V14®, aplicados a um estudo de caso que contempla uma edificação
residencial de 15 pavimentos. Os carregamentos, materiais, combinações e demais
parâmetros utilizados no estudo de caso foram pautados conforme a Norma
Regulamentadora NBR 6.118/2014 [1]. Os resultados de saída avaliados foram: momentos fletores positivos
e negativos máximos das
lajes, flechas máximas das lajes, tempo de processamento em cada software
para estrutura modelada e o número de nós gerado em cada método.
2
Fundamentação
Teórica
A análise estrutural de uma construção ou de seus elementos corresponde à
fase de idealização do comportamento estrutural, onde são considerados aspectos
como: tensões, deformações e deslocamentos da estrutura [2]. É nessa fase que há a determinação
dos esforços internos e externos, dos deslocamentos verticais e horizontais e
da deformação do conjunto estrutural a ser dimensionado. Martha [2] relata que a análise estrutural
moderna trabalha com quatro níveis de abstração (Figura 1), sendo o primeiro
nível correspondente à estrutura física, o segundo nível corresponde ao modelo
estrutural, ou seja, a estrutura real acrescida da idealização de seu
comportamento, o terceiro nível corresponde ao modelo discreto utilizado e os
diversos parâmetros do modelo estrutural, e o quarto nível que representa o
modelo computacional, isto é, o modelo discreto que será convertido em modelo
computacional através de sua implantação em um software.
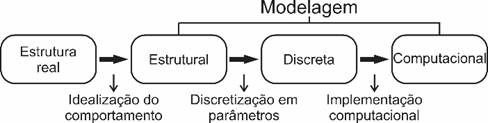
Figura 1: Níveis de abstração referentes a análise estrutural.
Fonte: adaptado
de Martha [2].
Atualmente, com o avanço de técnicas matemáticas e computacionais, há uma
melhor compreensão das estruturas, evitando superdimensionamento e reduzindo os
custos associados. Dentre as técnicas computacionais mais utilizadas para resolução
de problemas estruturais associados às lajes, destacam-se os métodos das
grelhas e elementos finitos (MEF).
2.1
Método
das grelhas
O método das
grelhas consiste na substituição do elemento laje por vigas nos sentidos
verticais e horizontais, encontrando-se perpendicularmente, formando uma grelha
(Figura 2), de modo que os esforços e os deslocamentos da laje são determinados
a partir desse conjunto de vigas [3].
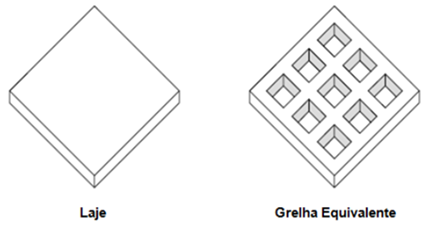
Figura 2: Esquema do método das grelhas – laje e
grelha equivalente.
Fonte:
Santos (2010).
Essa técnica
foi inicialmente idealizada por Marcus [4], que não dispunha na época de recursos computacionais
avançados e buscava um processo aproximado para dimensionamento de lajes. Em 1959, percebendo que as análises de
grelhas e pórticos planos pelo método dos deslocamentos eram bastante
parecidas, Lightfoot
e Sawko [5]
adaptaram um
algoritmo computacional para cálculo de pórtico plano usando o método das
grelhas.
Segundo Hambly [6], um painel de laje é estruturalmente
contínuo nas duas dimensões do plano da laje, de modo que as cargas aplicadas
são equilibradas por uma distribuição bidimensional de esforços cortantes,
momentos fletores e de torção. Como a solução rigorosa das equações
diferenciais raramente é possível, um procedimento aproximado pode ser usado, a
analogia de grelha, na qual o painel de lajes é representado para fins de
análise por uma grelha bidimensional de vigas. Os avanços significativos
realizados pelos programas de analogia de grelha nos últimos anos tornam esse
procedimento mais versátil, rápido, e simples de compreender do que os demais [7,8,9].
Para a análise
da grelha de forma completa, é fundamental que sejam determinados os números de
nós e barras (Figura 3) [10]. Não existe uma regra clara para o espaçamento entre as barras. Quanto menor o espaçamento, maior a
probabilidade da representação real do comportamento estrutural.
Vale ressaltar
que no método das grelhas as cargas são distribuídas linearmente ao longo das
vigas (kN m-1) enquanto que no MEF as cargas são bidimensionais
(kN m-2), posteriormente linearizadas pelo software.
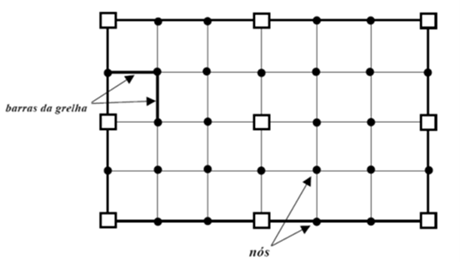
Figura 3: Barras e nós em uma laje hipotética.
Fonte: Hennrichs
(2003).
O processo de analogia de grelha vem sendo muito
empregado em programas computacionais de análise de estruturas de concreto
armado, como o Eberick, com grande aceitação no meio profissional. Esse
processo fornece ao projetista subsídio para a escolha do modelo estrutural que
melhor ajusta à situação real, permitindo a análise de um mesmo pavimento sob
diferentes situações, possibilitando adaptações em um mesmo conjunto de dados.
Na
Engenharia Civil, o método das grelhas pode ser utilizado para os diversos tipos
de lajes, como em Cavalcanti e Horowitz [11] que aplicou o método para verificação de flexão em um
tabuleiro de ponte sujeita à protensão.
2.2
Método
dos Elementos Finitos (MEF)
O MEF é normalmente utilizado para solucionar problemas
que envolvem e necessitam resolver Equações Diferenciais Parciais (EDP)
amplamente necessárias em Engenharia Estrutural [12,13,14,15], viabilizando também
outros tipos de análises como: térmicas, acústicas, dinâmica, eletromagnética e
de fluídos. Em problemas estruturais, a solução
pelo MEF é encontrada após discretização da estrutura em várias regiões
geometricamente delimitadas por nós. Essas regiões podem assumir diversas
formas, como: triângulos, retângulos ou outras estruturas não lineares. Para
cada região discretizado do problema é obtido uma solução numérica. O processo
numérico utilizado para resolução de problemas estruturais é detalhado por
Azevedo [16].
Pesquisas
utilizando MEF são amplamente desenvolvidas, sobretudo para resolução de
problemas não lineares. O grupo de pesquisa de Greco [12] estudou a utilização de aplicações não
lineares, utilizando o
MEF, para treliças espaciais, aplicando o método para quatro situações [10]. A comparação entre resultados
obtidos por MEF e métodos já consolidados, também são amplamente estudados,
como em
Junges e Rovere [17] que
comparou os resultados de flechas em vigas obtidos pelo MEF e métodos
normatizados.
3
Estudo
de Caso
O
edifício considerado no estudo de caso é constituído por pavimento térreo, treze pavimentos tipos e
cobertura, totalizando quinze pavimentos. As principais considerações e
características do projeto arquitetônico são descritos na Tabela 1.
Tabela
1: Principais características do edifício
local de estudo.
|
Destinação da edificação
|
Residencial multifamiliar
|
|
Tipo de estrutura
|
Concreto armado
|
|
Número de pavimentos
|
Quinze (15)
|
|
Área construída (m²)
|
23.379,60 m²
|
|
Altura total (m)
|
47,00 m
|
|
Pé-direito do pavimento tipo (m)
|
2,88 m
|
O sistema
estrutural do edifício é composto por elementos de concreto armado e todas
características dos materiais empregados estão apresentadas na Tabela 2.
Tabela
2: Propriedades dos materiais empregados
na análise estrutural.
|
Propriedades do concreto classe C35 ou 35 MPa
|
|
Resistência à compressão
|
|
Resistência característica (fck)
|
35,00 MPa
|
|
Coeficiente de minoração (yc)
|
1,4
|
|
Resistência de cálculo (fcd)
|
25,00 MPa
|
|
Características do concreto
|
|
Peso específico
|
25,00 kN m-3
|
|
Módulo de elasticidade (a partir do fck)
|
|
Módulo de elasticidade inicial (Eci)
|
33 GPa
|
|
Módulo de elasticidade secante (Ecs)
|
29 GPa
|
|
Resistência a tração (a partir do fck)
|
|
Resistência média (fctm)
|
3,21 MPa
|
|
Resistência característica inferior (fctk, inf)
|
2,25 MPa
|
|
Resistência característica superior (fctk, suo)
|
4,17 MPa
|
|
Resistência de cálculo (fctd)
|
1,60 MPa
|
|
Propriedades do aço classe CA50 ou 500 MPa
|
|
Resistência característica de escoamento (fy)
|
500 MPa
|
|
Coeficiente de minoração (yaço)
|
1,15
|
|
Resistência de cálculo (fyd)
|
434,78 MPa
|
|
Limite de resistência (fst)
|
478,26 MPa
|
|
Propriedades do aço classe CA60 ou 600 MPa
|
|
Resistência característica de escoamento (fy)
|
600 MPa
|
|
Coeficiente de minoração (yaço)
|
1,15
|
|
Resistência de cálculo (fyd)
|
521,74 MPa
|
|
Limite de resistência (fst)
|
573,97 MPa
|
|
Coeficiente de minoração (yaço)
|
1,15
|
|
Resistência de cálculo (fyd)
|
521,74 MPa
|
|
Limite de resistência (fst)
|
573,97 MPa
|
As Figuras 4 e
5 ilustram a arquitetura do pavimento tipo do empreendimento em estudo, evidenciando
a formatação e disposição das lajes para modelagem e dimensionamento,
respectivamente.
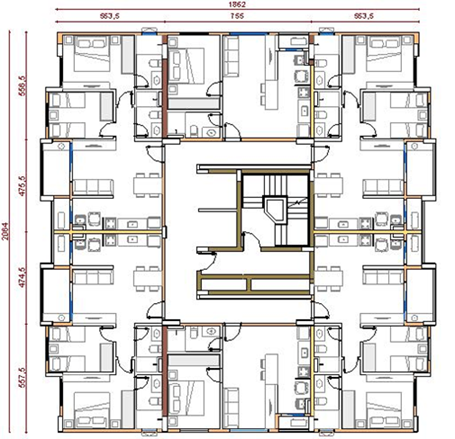
Figura 4: Planta baixa e layout do pavimento tipo elaborado no software
Revit®.
Fonte: Autoria própria.
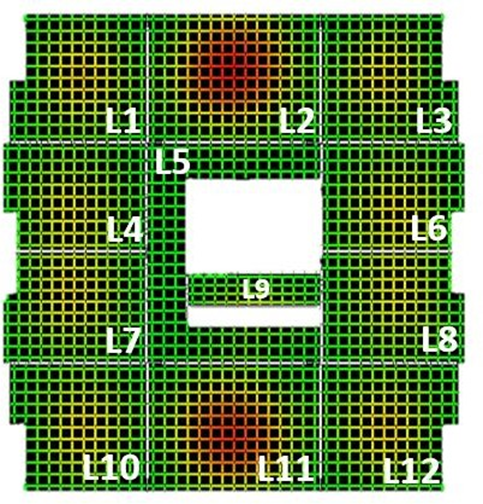
Figura 5: Esquema das lajes do pavimento tipo implementado no software
Eberick V8®.
Fonte: Autoria própria.
Na Tabela 3
são relatadas as cargas acidentais e permanentes consideradas, considerando as
recomendações da Norma Regulamentadora NBR 6.120/2019 [18].
Tabela
3: Levantamento das cargas acidentais e permanentes
conforme projeto arquitetônico (NBR 6.120/2019 [18]).
|
Tipo de edificação
|
Tipo de carga
|
Ambiente
|
Carga (kN m-2)
|
|
Edifício residencial
|
Acidental
|
Dormitórios, sala, copa, cozinha e banheiro
|
1,50
|
|
Despensa, área de serviço e lavanderia
|
2,00
|
|
Corredor com acesso ao público
|
3,00
|
|
Permanente
|
Argamassa
|
0,63
|
|
Argamassa em gesso
|
0,25
|
|
Porcelanato
|
0,15
|
4
Metodologia
Inicialmente,
o projeto arquitetônico foi analisado e realizou-se a contabilização dos
ambientes, elementos estruturais e materiais utilizados a fim de fazer o
levantamento das cargas solicitantes para o dimensionamento das lajes, conforme
preconiza a
NBR 6.120/2019 [18].
Para o cálculo
da composição da carga das alvenarias, foram consideradas espessura de 15 cm,
densidade aparente de 13,0 kN m-3 e pé-direito do pavimento
tipo de 2,88 m (conforme projeto arquitetônico).
A NBR
6.118/2014, item 11.8, recomenda que as combinações dos esforços devem
contemplar a situação mais desfavorável na estrutura para o estado limite
último (ELU) e o estado limite de serviço (ELS) [1]. Assim, foram consideradas todas as
ações atuantes no elemento estrutural laje: ação decorrente do peso próprio e
carga adicional (ação permanente), ação acidental, bem como os coeficientes de
ponderação e fatores de combinação (Tabela 4), de modo que obteve-se as
combinações de cargas atuantes (Tabela 5).
Tabela
4: Tipologia, coeficiente e fatores de
combinação dos carregamentos empregados na análise estrutural.
|
Tipo
|
Ação
|
Indicação
|
Coeficiente de ponderação
|
Fatores de combinação
|
|
Favorável
|
Desfavorável
|
y0
|
y1
|
y2
|
|
Permamente
|
Peso próprio
|
PP
|
1
|
1,3¹
|
1
|
1
|
1
|
|
Permamente
|
Adicional
|
PERM
|
1
|
1,4
|
1
|
1
|
1
|
|
Acidental
|
Adicional
|
SC
|
0
|
1,4
|
0,5
|
0,4
|
0,3
|
1 Para cargas permanentes de pequena
variabilidade, como o peso próprio das estruturas, esse coeficiente pode ser
reduzido para 1,3.
Tabela
5: Combinação de ações para o ELU.
|
Combinação
|
Ações constituintes
|
|
Combinação 1
|
1,3PP + 1,4PERM
|
|
Combinação 2
|
1,3PP + 1,4PERM + 0,98SC
|
|
Combinação 3
|
1,3PP + 1,4PERM + 1,4SC
|
Em se tratando
de projeto de edificação residencial, recomenda-se a utilização de fatores de
combinação menores, tendo em vista ser um local onde não há grande presença de
peso de equipamentos, porém, nesse trabalho, optou-se por utilizar valores
maiores, conforme apresentado na Tabela 4. As combinações e ações foram
inseridas como dados de entrada nos softwares, de forma que, após o
processamento da estrutura, a combinação mais desfavorável foi considerada para
a estrutura a partir das possibilidades de combinação apresentadas na Tabela 5.
Após realizado
o levantamento das cargas impostas e informações necessárias para o
pré-dimensionamento das peças, toda estrutura de concreto armado foi analisada nos softwares Eberick V8® e SAP2000 V14® com a
finalidade de dimensionar as peças, sendo que o primeiro utiliza o método das
grelhas, enquanto que o segundo utiliza o MEF. Em ambos programas utilizou-se
os mesmos parâmetros de contorno, cargas solicitantes, materiais constituintes,
combinações e o coeficiente de Poisson de 0,2. As análises foram lineares. Para
o MEF, as lajes foram discretizadas em quadrados e foram gerados 3498 nós. Para
o método das grelhas foram utilizados 2012 nós.
As condições de contorno empregadas na
interface laje-viga foram do tipo engastadas. As vigas conectaram-se com outras
vigas e pilares através do engastamento da peça, havendo transferência de
momentos e esforços.
Para
possibilitar a comparação entre os métodos, buscou-se avaliar os seguintes
parâmetros, de forma quantitativa, qualitativa e orçamentária:
• momentos
positivos e negativos máximos das lajes;
• flechas
máximas das lajes, de forma percentual;
• tempo de
processamento da estrutura;
• número de
nós gerados por cada software.
A variação de
temperatura foi desconsiderada no processamento de dimensionamento da
estrutura.
Para análise
das deformações, foi considerado o Estado Limite de Serviço (ELS), estado em
que a estrutura possui condições adequadas de segurança, funcionalidade e durabilidade,
comparando os valores admissíveis com os valores de deformações obtidos. A
flecha máxima, também chamada de deslocamento-limite, foi o parâmetro de
deslocabilidade adotado e o seu valor limite foi considerado a partir da
aceitabilidade sensorial – definida como o limite para ocorrência de vibrações
indesejáveis e efeito visual desagradável, conforme a NBR 6.118/2014 [1]. Na situação apresentada, a NBR
6.118/2014 [1]
estabelece que o
valor limite das flechas deverá ser de l/250, sendo l a maior
dimensão da laje.
Para análise
dos custos foi utilizado o parâmetro de taxa de aço, tanto para armaduras
positivas quanto negativas de cada laje. O custo de concretagem não foi
incluído no cálculo, tendo em vista seu baixo impacto comparado as armaduras de
aço. Para o cálculo da taxa de armadura foram utilizadas as Equações 1 a 5 [1]:
em que: As
é a área do aço [L2], Md é o momento fletor de
cálculo [FL], z é o braço de alavanca [L], fyd é a
resistência a tração do aço reduzido da minoração normativa [FL-2], d
é altura útil da peça [L], x é a posição da linha neutra [L], bw
é base da seção transversal da laje, fcd é a resistência à
compressão do concreto reduzido da minoração normativa [FL-2].
5
Resultados
5.1
Flechas
máximas
Na Figura 6
são apresentados os resultados de flechas máximas obtidas pelos métodos das
grelhas e elementos finitos, que foram utilizados para as lajes dimensionadas
(L1 a L12). Nas combinações de entrada inseridas em ambos softwares,
nota-se que foram desprezadas as ações quase permanentes, ações variáveis de
longa duração que podem atuar em pelo menos metade da vida útil da estrutura.
Portanto, as flechas calculadas foram do tipo imediata, uma vez que estas não
contemplam ações quase permanentes, além da fluência do concreto. Quanto a
fissuração, no método das grelhas houve consideração, porém no MEF a fissuração
da peça não foi considerada diretamente, ocorrendo através da diminuição do
valor de módulo de elasticidade Ecs. Os maiores valores de
flecha máxima foram encontrados nas lajes L2 e L11, ambas simétricas. Esse fato
se deve aos maiores vãos existentes nessas lajes, ressaltando que nenhuma dos
valores de flechas foram superiores aos prescritos na NBR 6.118/2014 [1].
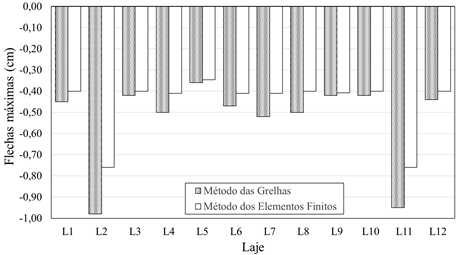
Figura 6: Flechas máximas para cada laje e método (software) de
dimensionamento.
Fonte: Autoria própria.
Os resultados
sobre as flechas máximas sugerem que o Eberick V8® possui um modelo bem
adaptado para concreto armado, em virtude da redistribuição dos esforços e
consideração, de forma direta, da fissuração do concreto na flecha, obtendo,
assim, valores maiores para o método das grelhas, em comparação ao MEF.
Observa-se
que, lajes com menores dimensões tendem a apresentar as mesmas flechas máximas
considerando os dois métodos utilizados (Figuras 5 e 6). Percebe-se, também,
que o aumento na dimensão das lajes tende a ser acompanhado pelo aumento na
diferença dos resultados, mostrando uma influência dessa variável sobre os
resultados obtidos entre os dois métodos.
5.2
Momentos
fletores
A Figura 7
ilustra os valores dos momentos fletores máximos positivos na direção
horizontal (x) e vertical (y), atuantes nas lajes L1 até L12.
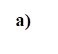
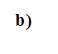
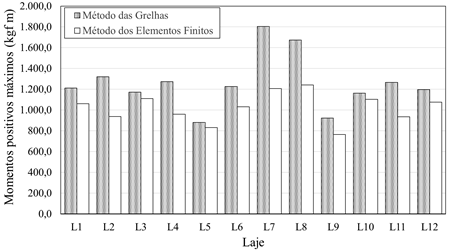
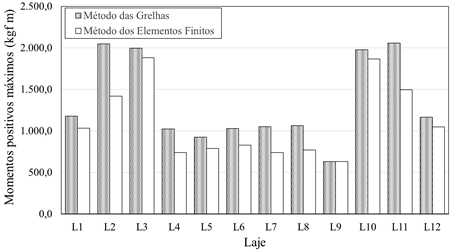
Figura 7: Momentos máximos positivos a) direção horizontal; b) direção
vertical.
Fonte: Autoria própria.
Na Figura 7a,
percebe-se que nas lajes L3, L5 e L10, os valores de momentos máximos positivos
na direção horizontal obtidos pelos dois métodos foram próximos (proximidade
entre a disposição da grelha e malha de elementos finitos). Isso pode estar
associado ao fato de que, essas três lajes delimitam um eixo de simetria na
direção horizontal diagonal do pavimento, além de que, esses menores
deslocamentos das lajes L3 e L10 se deve a presença de pilares nos quatro
cantos, haja visto que foram simplesmente apoiados. Já na Figura 7b, percebe-se
que os maiores valores de momento máximo positivo vertical ocorrem nas lajes
L2, L3, L10 e L11, ambas com maiores vãos e localizadas nas extremidades do
pavimento.
A Figura 8
apresenta os valores de momentos máximos negativos na direção horizontal (x)
e vertical (y).
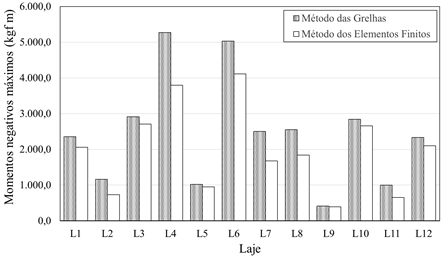
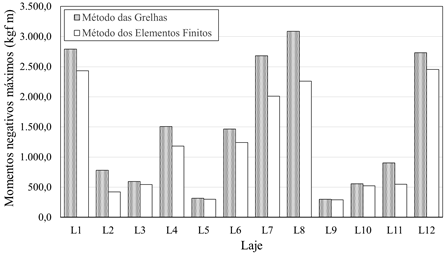
Figura 8: Momentos máximos negativos a) direção horizontal; b) direção
vertical.
Fonte: Autoria própria.
Na Figura 8a,
percebe-se que os maiores valores de momento negativo no sentido horizontal
ficaram concentrados nas lajes L4, L6, L7 e L8, pertencentes à porção central
do pavimento. Esse fato se deve, pois, essas lajes não possuem pilares em todos
os cantos alterando a distribuição de inércia do pavimento.
Durante o
processamento e análise dos resultados apresentados na Figuras 8, percebe-se
que os momentos fletores negativos mais representativos correspondem aos
esforços provenientes da geometria irregular da laje situados nos limites dos
elementos estruturais. Devido ao mapeamento nodal realizado pelo MEF, o excesso
de esforço devido aos momentos foram reduzidos, tendo em vista a melhor
discretização do pavimento, enquanto que o elemento grelha realiza ponderações
a favor da segurança, majorando os esforços.
5.3
Análise
qualitativa
A análise
qualitativa visa comparar os parâmetros relevantes considerados não técnicos mais
que podem impactar diretamente na performance e velocidade de desenvolvimento
do projeto, além de destacar as vantagens e desvantagens mais significantes de
cada método e software utilizado. Na Tabela 6 são apresentados esses
resultados qualitativos, destacando maior número de nós e tempo de
processamento para o MEF, enquanto a Tabela 7 lista as vantagens e desvantagens
de cada método.
Tabela
6: Número de nós gerados e tempo de
processamento para cada método (software) utilizado.
|
|
Método das Grelhas
|
Método dos Elementos Finitos
|
|
Tempo de processamento
|
00:06:09
|
00:13:10
|
|
Número de nós
|
2012
|
3498
|
Tabela
7: Considerações sobre os métodos
utilizados.
|
Método das Grelhas
|
Método dos Elementos Finitos
|
|
Vantagem
|
Desvantagem
|
Vantagem
|
Desvantagem
|
|
Não exige hardware avançado para processamento
|
O cálculo dos esforços e flechas é realizado nas barras
|
A malha refinada minimiza esforços residuais ou esforços não
condizentes com o real comportamento da estrutura, por exemplo: momento mais
condizente com o comportamento real
|
Número de nós superior ao proposto pelo método das grelhas, o que
exige processamento mais avançado
|
|
Resultados satisfatórios em estruturas regulares
|
As cargas são aplicadas somente nas barras
|
O cálculo dos esforços e flechas são realizados nos nodais
|
Tempo elevado de processamento devido a malha mais refinada
|
|
Dimensionamento a favor da segurança
|
-
|
Os vetores de carga são nodais
|
-
|
O equipamento
utilizado para as análises foi um notebook dotado de: processador Intel® Core™
i7-7500U, CPU @2.70GHz 2.90GHz, 8.00GB memória RAM e placa de vídeo NVIDIA® GEFORCE
940MX.
Percebe-se que
a utilização do método das grelhas dispende um menor custo computacional e número
de nós, consequentemente, demandando um menor tempo de processamento. Entretanto,
através dos resultados discutidos na seção 5.1 e 5.2, percebe-se que esse baixo
custo computacional pode estar associado pela menor discretização adotada para
os domínios, influenciando a distribuição dos esforços solicitantes e
consequentemente, majoração das peças estruturais. Já o MEF, demandou maior gasto
computacional, porém, com maior refinamento nos resultados do ponto de vista
econômico.
5.4
Análise
dos custos das armações
Na Figura 9a é
apresentado o consumo de aço, em massa total, necessário para execução das
lajes e a Figura 9b o comparativo de custo dessas armações por pavimento para
cada método utilizado. A base de dados de preço das composições de custo e
insumos utilizadas para quantificar o custo total foi a do Sistema Nacional de
Pesquisa de Custos e Índices da Construção Civil (SINAPI), tendo como data base
o mês de março, ano 2020, desonerado.
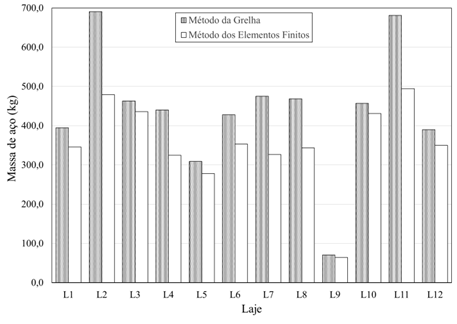
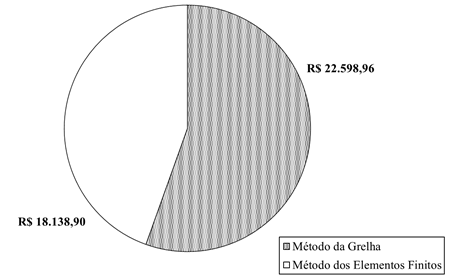
Figura 9: Quantitativo do aço e custos associados a cada método utilizado
a) massa de aço para cada laje; b) custo de armadura das lajes por pavimento,
considerado base dados SINAPI 03/2020, desonerado.
Fonte: Autoria própria.
Na Figura 9a,
percebe-se que, para todas as lajes apresentadas, houve um menor consumo de aço
necessário quando considerado o MEF, em comparação ao método das grelhas. A
Figura 9b reforça a afirmação anterior em termo de custos pois percebe-se uma
redução de mais de 19% entre o MEF e o método das grelhas, gerando uma economia
de aproximadamente
R$ 4.460,06 por pavimento, ou R$ 66.900,90 para a edificação total. Além dos
custos com o aço serem
menores, o MEF apresentou valores de momentos e flechas inferiores em relação à
análise por grelhas. Resultados semelhantes foram obtidos por Lorenci [19], que em seus estudos obteve a
utilização de quantidades menores de aço em comparação com métodos
simplificados de normas, evidenciando que o MEF é um método de dimensionamento
menos conservador.
A economia
gerada pela comparação entre os dois diferentes métodos utilizados para o
dimensionamento das peças estruturais não impactará na segurança e durabilidade
do empreendimento, ressaltando que ambos os métodos levam em consideração o
estado último de serviço e o estado limite último. Apesar do MEF requerer um
maior tempo de processamento para o dimensionamento estrutural, neste caso,
aproximadamente sete minutos a mais (Tabela 6), do ponto de vista dos ganhos
econômicos, houve significativa redução de custo (Figura 9).
6
Conclusões
Percebe-se que
os valores obtidos através do método das grelhas, seja os deslocamento ou
momentos fletores, foram superiores em relação ao método dos elementos finitos,
demostrando ser um pouco mais conservador para o dimensionamento estrutural de
concreto armado quando comparado ao método dos elementos finitos (MEF). Apesar de
sua praticidade de execução e não exigência de grande custos computacionais, as peças
estruturais dimensionadas pelo método das grelhas tiveram os custos mais
elevados associados aos maiores valores de cargas obtido pelo método.
Considerando
que a laje é o elemento
estrutural que mais demanda aço em uma obra, conforme relata Jablonski [20], uma significativa redução na
quantidade de aço gera grande impacto no orçamento de uma edificação, corroborada pela
proporcionalidade à quantidade de pavimentos.
O
MEF tem se mostrado uma excelente alternativa para projetos estruturais de
concreto armado, com maior potencial de detalhamento e refinamento da malha de
elementos finitos para as peças estruturais em relação aos métodos
tradicionais, consolidados e normatizados.
Pode-se
concluir com esse estudo que, o MEF mostrou ser eficiente para o dimensionamento
de lajes, sobretudo para edificações de múltiplos pavimentos, principalmente no
que diz respeito a quantidade de aço necessária e segura, consequentemente, menores
custos associados a esse material.
Recomenda-se
que softwares que possuem o método das grelhas em sua base sejam
aplicados e direcionados para as pequenas edificações, com menores vãos e
complexidade, onde não há tanta repetibilidade e quantidade de ligações e peças
estruturais, sendo seu uso confiável e seguro da mesma forma que softwares
que utilizam o MEF.
Referências
[1] ABNT - ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118:2014 – Projeto
de Estruturas de Concreto Armado - Procedimento, Rio de Janeiro, RJ, 2014.
[2] MARTHA, L. F. Métodos Básicos da Análise de Estruturas. Rio de
Janeiro: PUC - Rio, 2007. 312 p.
[3] SANTOS, L. F.
C. Comparação de Modelos de Grelha e de Elementos Finitos de Laje na
Modelação de Estruturas de Edifícios de Betão Armado: Dissertação de
Mestrado em Engenharia Civil. [S.L.: s.n.], 2010.
[4] STRAMANDINOLI, J. S. B. Contribuições à Análise de Lajes Nervuradas
por Analogia de Grelha: Dissertação de Mestrado em Engenharia Civil.
Florianópolis: Universidade Federal de Santa Catarina (UFSC), 2003.
[5] LIGHTFOOT, E.; SAWKO. F. Structural frame analysis by eletronic computer: grid
frameworks resolved by generalized slope deflection. [S.L.: s.n.], 1959.
[6] HAMBLY, E. C. Bridge deck behavior.
London, Chapman and Hall: [s.n.], 1976.
[7] STRAMANDINOLI, J. S. B.; LORIGGIO, D. D. Estudo da rigidez à
torção para a aplicação do processo de analogia de grelha em lajes maciças. In:
V Simpósio EPUSP sobre estruturas de concreto, v. 88040, p. 900, 2003.
[8] DÓRIA, L. E. S.; LIMA, F. B. Análise de fundação tipo radier empregando
o modelo de analogia de grelha. In: Congresso Brasileiro do Concreto, p.
15, 2008.
[9] CARLESSO, G. C.; FOLLETTO, E. P.; SILVA, V. O. Utilização da
analogia de grelha para análise de lajes maciças em concreto armado.
Seminário de Iniciação Científica, Seminário Integrado de Ensino, Pesquisa e
Extensão e Mostra Universitária, 2019.
[10] HENNRICHS, C. A. Estudos Sobre Modelagem de Lajes Planas de
Concreto Armado. Dissertação de Mestrado em Engenharia Civil.
Florianópolis: Universidade Federal de Santa Catarina (UFSC), 2003.
[11] CAVALCANTI, M. B.; HOROWITZ, B.
Modelos de verificação à flexão de estruturas protendidas. Rev. IBRACON
Estrut. Mater., São Paulo, v. 1, n. 4, p. 331-364, Dec. 2008. https://doi.org/10.1590/S198341952008000400002.
[12]
GRECO, M.; GESUALDO, F. A. R.; VENTURINI,
W. S.; CODA, H. B. Nonlinear positional formulation for space truss analysis. Finite elements in analysis and design, v. 42, n. 12, p. 1079-1086, 2006.
[13] STRAMANDINOLI, R. S. B.; ROVERE, H. L. Modelo de elementos finitos
para análise não linear de vigas e pórticos planos de concreto armado. Revista IBRACON de Estruturas e Materiais, v. 10, n. 2, p. 386-414, 2017.
[14]
WANG, Y.; LU, Y. J.; SI, C. D.; SUN, T. C.
Finite element analysis for rutting prediction of asphalt concrete pavement
under moving wheel load. International Journal of Simulation Modelling,
v. 16, n. 2, p. 229-240, 2017.
[15]
LIU, Y.; XIAO, H.; YAO, K.; HU, J.; WEI, H.
Rock-soil slope stability analysis by two-phase random media and finite
elements. Geoscience Frontiers, v. 9, n. 6, p. 1649-1655, 2018.
[16] AZEVEDO, A. N. Método dos Elementos Finitos. 1 ed.
Portugal: Faculdade de Engenharia da Universidade de Porto, 2003.
[17] JUNGES, E.; ROVERE, H. L. Comparação entre modelos simplificados e
de elementos finitos para flecha imediata em vigas contínuas de concreto
armado. Revista IBRACON de Estruturas e Materiais, v. 10, n. 2, p.
415-450, 2017.
[18] ABNT - ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6120:2019 –
Cargas para Cálculo de Estruturas de Edificações - Procedimento, Rio de
Janeiro, RJ, 1980
[19] LORENCI, G. V. S. Lajes lisas protendidas: comparação dos
métodos de dimensionamento à flexão. Trabalho de Conclusão de Curso
(Bacharelado em Engenharia Civil). Porto Alegre: Universidade Federal do Rio
Grande do Sul (UFRGS), 2010.
[20] JABLONSKI, L. Índices e Taxas de Consumo de Materiais em Função
da Tipologia Estrutural. Trabalho de Conclusão de Curso de Engenharia
Civil. Alegrete: Universidade Federal do Pampa (UNIPAMPA), 2013.
orcid.org/0000-0002-2821-7717
orcid.org/0000-0001-6814-8026
orcid.org/0000-0001-6910-5722
orcid.org/0000-0002-1158-9661