1
Introdução
As estruturas
mistas têm o objetivo de aproveitar as vantagens de cada um dos elementos
utilizados (aço e concreto), não apenas em termos estruturais, mas também em
aspectos construtivos, funcionais e estéticos. O funcionamento das estruturas
mistas de aço-concreto é garantido de maneira mais frequente através de
interação mecânica por conectores de cisalhamento, soldados à viga metálica e embutidos
na laje de concreto.
Em um piso
misto convencional, a laje de concreto é posicionada sobre o flange superior da
viga de aço. Desta forma, uma das características principais desse sistema é sua
elevada altura total, decorrente da soma da altura da viga e da espessura da laje
de concreto, o que pode ocasionar uma limitação do pé-direito do pavimento. Por
outro lado, o sistema de pavimento misto de pequena altura, Slim Floor,
entre outros aspectos, visa a redução dessa altura apoiando a laje sobre o
flange inferior da viga de aço, como apresentado na Figura 1.
Além disso, no cenário atual das construções metálicas e mistas, tem crescido
significativamente a importância do projeto estrutural que apresente maior durabilidade
em condições de incêndio, o que faz com que o sistema Slim Floor seja
bastante atrativo devido à sua capacidade resistente ao fogo, visto que as
vigas metálicas estão parcialmente revestidas pelo concreto.

Figura
1: Perfil ASB
constituindo o sistema Slimdek. Fonte: Ramos [1].
A utilização
de estruturas mistas no Brasil deu-se, inicialmente, utilizando-se de manuais e
normas internacionais para construção de alguns edifícios e pontes de pequeno
vão entre as décadas de 1950 e 1960. Entre 1970 e início dos anos de 1980, foi
notada uma estagnação da utilização dos sistemas mistos de aço-concreto no
país. Isso possivelmente ocorreu devido à opção ao uso de estruturas e métodos
convencionais, situação que ainda é verificada atualmente, e à necessidade de
profissionais qualificados em seu projeto e execução (MALITE [2]).
A norma NBR
8800 ABNT de 2008 [3] abrange
o comportamento e critérios de dimensionamento para vigas, pilares e lajes
mistas de aço-concreto, sem, no entanto, abordar explicitamente o sistema misto
de pequena altura. Desta forma, destaca-se a importância dos estudos das
estruturas mistas e dos pavimentos mistos de pequena altura em relação ao seu
comportamento durante toda a sua vida útil, para melhora das técnicas
construtivas e o consequente aperfeiçoamento dos princípios de projeto deste
sistema, bem como para possibilitar a elaboração de normas para o sistema Slim
Floor (KOCHEN [4]).
No caso das
estruturas Slim Floor, quando não prevista a utilização de conectores de
cisalhamento, se torna necessária a consideração da interação entre o aço e o
concreto através do atrito gerado por ranhuras que podem ser dispostas no
perfil metálico, e ainda outras formas de ativação desta aderência (HOU [5]), pois neste arranjo, o perfil
metálico tem uma região de contato muito superior quando comparada aos sistemas
mistos tradicionais.
O modelo
objeto de validação para os estudos em Slim Floor do presente trabalho
foi desenvolvido experimentalmente pelo Steel Construction Institute – SCI e
British Steel (atual Tata Steel) no Reino Unido, através de ensaios com perfis
do tipo Asymmetric Slim Flor Beam – ASB, ligados a uma laje mista (LAWSON
et al. [6]). Esse estudo foi realizado para
determinar o momento fletor resistente da viga mista e a tensão última de
aderência na interface aço-concreto.
Paes [7] apresentou um estudo do sistema Slim
Floor constituído de vigas com ranhuras dispostas na aba superior do perfil
metálico, via Métodos dos Elementos Finitos. Analisou os modelos SCI – 280 ASB,
com as dimensões demonstradas na Figura 2,
e 300 ASB, obtendo resultados muito próximos aos resultados experimentais. Considerou
em seu estudo as propriedades do concreto, tais como a fluência e retração.
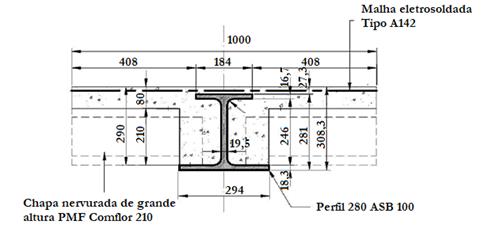
Figura
2. Dimensões do modelo. Fonte: Lawson et
al. [6] apud Paes [7].
Para
representação da interface aço-concreto, Paes [7] realizou em seu estudo uma
reinterpretação dos estudos feitos por Leskelä e Hopia [8], em que foram analisados quatro
diferentes tipos de conexão de cisalhamento para estruturas de Slim Floor:
alma lisa; alma com ranhuras superficiais; alma lisa com barras de aço
passantes e, por fim, alma com ranhuras superficiais e barras de aço passantes.
Como pode ser visto em outros trabalhos sobre modelagens numéricas de sistemas Slim
Floor, as principais dificuldades encontradas remetem à representação das
várias interfaces entre o aço e o concreto, bem como o comportamento do
concreto em si, e ainda, as diferentes formas em ativar este comportamento
misto do aço e concreto (LAM [9]; CHEN [10];
SHEEHAM ET AL. [11]; SCHORR
e KUHLMANN [12]; BALDASSINO ET AL. [13]; ROCHA E MUNAIAR NETO [14]).
A modelagem
numérica permite maior possibilidade de estudos, sem a necessidade do elevado
custo inerente à realização de ensaios experimentais. Este trabalho apresenta a
análise de um sistema de piso misto de pequena altura via elementos finitos, no
software ANSYS [15],
com ênfase na atribuição das propriedades do concreto armado e nas
possibilidades de implementação da interface aço-concreto, tendo como
referência resultados experimentais disponíveis na literatura (LAWSON et al. [6]).
2
Análise
numérica
A geometria do modelo foi feita a partir da geração dos volumes no ANSYS [15]. A malha de elementos finitos foi
feita a partir dos volumes criados, buscando aliar a precisão e a eficiência
computacional. A malha de elementos finitos é apresentada na Figura 3.
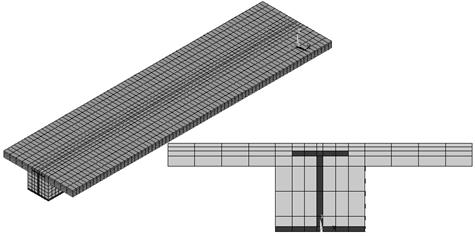
Figura
3. Malha de elementos
finitos.
Os elementos finitos adotados nesta pesquisa pertencem à biblioteca
interna do ANSYS [15].
O elemento utilizado para simular o comportamento do perfil metálico foi o solid186, com vinte nós, sendo três
graus de liberdade por nó: translações nos eixos x, y e z. Esse elemento é
capaz de ser associado a materiais com comportamento não linear e ainda permite
simular o comportamento plástico, além de outras características que não serão
utilizadas para este estudo.
Para representação da laje de concreto, foi utilizado o elemento solid65, com oito nós, e três graus de
liberdade em cada nó. Esse elemento é capaz de simular os esforços de tração e
compressão, podendo ser visualizado inclusive o detalhamento dos primeiros
pontos de fissuras ocorridas na laje. O elemento permite ainda a inclusão de
armadura através de taxas. Tais armaduras podem ser dispostas em até três
direções distintas. Neste trabalho, as armaduras da laje de concreto foram
inseridas através de taxas, com suas propriedades mecânicas adicionadas como
forma de constantes reais atribuídas ao elemento de concreto.
Foram utilizadas duas alternativas para a simulação da interface
aço-concreto. Uma das alternativas, baseada no trabalho realizado por Paes [7], foi o elemento combin39, que é um elemento de mola
unidirecional que possui capacidade longitudinal ou torcional. Para sua opção
longitudinal, utilizada neste trabalho, é um elemento de compressão-tração
uniaxial com até três graus de liberdade por nó – translações nas direções x, y
e z e grande capacidade de deslocamento. Para a utilização deste elemento de
mola é necessário informar ao programa a relação de força versus deslizamento (PAES
[7]), representando seu comportamento longitudinal,
sendo os demais deslocamentos impedidos. Foram criados elementos de mola com
rigidez à translação na direção longitudinal do modelo. Em todos os nós foi feito
o acoplamento dos deslizamentos nas direções ortogonais ao eixo da estrutura
para impedir o deslocamento de corpo rígido.
A outra alternativa foi a utilização de elementos de contato targe170 e conta173 para representar a interação na superfície de
interface aço-concreto. Tais elementos podem ser utilizados em análises
tridimensionais com contato tipo superfície-superfície, sendo o elemento targe170 definido para a superfície
alvo, mais rígida, e o elemento conta173
para a superfície de contato, mais deformável (MARCONCIN [16]). Para representar a superfície
correspondente ao concreto, foi utilizado o targe170,
já para a superfície do perfil metálico, o conta173.
Para representação da interface aço-concreto através dos elementos de
contato foram utilizados os valores adotados por Kotinda [17] para as regiões de encontro dos dois
materiais, em que o perfil metálico possui superfície lisa, e, com a finalidade
de melhorar a convergência do modelo, encontraram-se em Oliveira et al. [18] parâmetros importantes para
representar a aderência entre o concreto e o aço.
Foram inseridos os valores do coeficiente de atrito (μ) e coesão (c), com
escorregamento regido pela Lei de Coulomb, descritos através da equação (1),
conforme proposto por Kotinda [17]. Ao se exceder a tensão cisalhante limite (τlim),
ocorre o deslizamento entre os materiais. O valor de P é a tensão normal.
τlim= μ∙P + c (1)
Os valores adotados foram coeficiente de atrito (µ) = 0,40, coesão (c) =
0,18 kN/cm², coeficiente de penetração (FTOLN) = 0,01, que, segundo Kotinda [17], refere-se a um valor mínimo de
penetração para que o status do contato seja considerado como fechado. Oliveira
et al. [18] apresentam ainda o parâmetro de fator
de rigidez normal FKN = 0,1, que segundo os autores, é o valor recomendado
quando a deformação predominante for de flexão. O mesmo valor de FKN foi
adotado para o fator de rigidez de tração FKT = 0,1. Para representação da
superfície onde existem as ranhuras no perfil metálico, com maior aderência
entre os materiais, foram adotados os mesmos parâmetros, com a única alteração
para coesão (c), em que foi utilizado o valor de 2,00 kN/cm². A Figura 4 apresenta os elementos de contato.
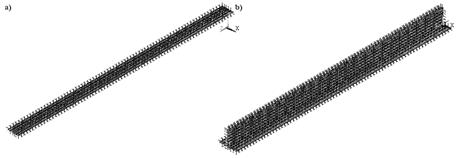
Figura
4. Interface
aço-concreto com elementos targe170 e conta173. a) superfície com ranhuras
superficiais no perfil metálico b) restante da interface lisa.
Para reduzir o tempo de análise computacional, foi utilizado o recurso de
simetria (ANSYS [15]),
que permite simular apenas a metade do sistema, sem impactos significativos nos
resultados. Logo, modelou-se a metade do vão original de 7500 mm, representado na Figura 5, adequando-se a aplicação de carga e as condições de
contorno.
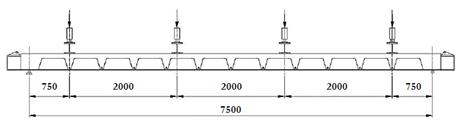
Figura
5. Dimensões do vão. Fonte: Lawson et
al. [6] apud Paes [7].
O carregamento foi aplicado de modo incremental, devido à não linearidade
física do material. Desta forma, o processamento foi subdividido em 100 etapas,
para melhorar a convergência do modelo.
As condições de contorno empregadas, representadas na Figura 6, foram restrições à translação nas direções vertical e
transversal, na região do apoio em uma das extremidades do modelo, no flange
inferior do perfil metálico. A Figura 6 apresenta a malha de elementos finitos, as condições de contorno e o
carregamento.
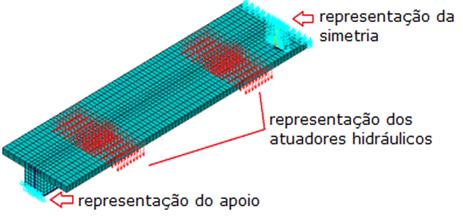
Figura
6. Condições de contorno
e aplicação das cargas.
Foi adotado o modelo multilinear para o concreto. Os valores do módulo de
elasticidade (Ec), coeficiente de Poisson (ν), resistência à
compressão (fck) e resistência à tração (fct) do concreto
foram utilizados conforme descrito por Paes [7], que considera as características de um concreto de
classe C35/40. Desta forma, foi adotado o valor de Ec = 35.000 MPa,
ν = 0,20, fck= 35 MPa e fct = 3,23 MPa.
No que se refere ao comportamento às tensões de tração, foi utilizada uma
relação constitutiva presente no ANSYS [15], concrete, baseado no modelo de Willan-Warnke. Os
parâmetros necessários à sua utilização foram apresentados no trabalho de Paes [7] e alguns outros parâmetros
permaneceram como pré-definidos pelo programa. Para o coeficiente de
transferência de cisalhamento para fissura aberta, foi utilizado o valor de 0,3;
para o coeficiente de transferência de cisalhamento para fissura fechada, o
valor de 1,00; e para o coeficiente multiplicador de rigidez para condição
fissurada na tração, foi utilizado o valor de 0,6.
Para obter a curva tensão-deformação para o concreto submetido à
compressão uniaxial, são utilizadas as equações (2) e (3) (MODEL CODE [19]). Para que este comportamento seja
ativado no ANSYS [15],
é necessário desabilitar a função de compressão no modelo concrete,
bastando para isso, informar o valor de -1 para a resistência à compressão no
modelo concrete.
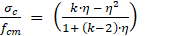 (2)
(2)
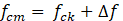 onde
onde 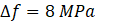 (3)
(3)
Onde:
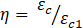 ,
, 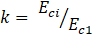
fcm
= resistência média à compressão,
fck = resistência característica à compressão do concreto,
𝜀𝑐 = deformação de compressão,
𝜀𝑐1 = deformação na máxima tensão de compressão,
𝑘 = número de plasticidade,
𝐸𝑐𝑖 = módulo de elasticidade inicial do
concreto;
𝐸𝑐1 = módulo secante da origem do pico de tensão de
compressão.
Para o perfil metálico, o aço utilizado no modelo experimental foi do
tipo S355, com comportamento elasto-plástico perfeito, em um modelo constitutivo
bilinear, com módulo de elasticidade (Es) de 210.000 MPa e
coeficiente de Poisson (ν), 0,30, e tensão de escoamento (fy) igual
a 410 MPa.
Para as armaduras, representadas no modelo experimental por uma malha
eletrosoldada A142, distribuída ao longo da parte superior da laje de concreto,
são considerados os mesmos valores para o módulo de elasticidade e coeficiente
de Poisson; já para tensão de escoamento, adotou-se o valor de 460 MPa. No
modelo numérico, as armaduras são inseridas por meio de taxas, iguais em ambas
direções, Asx = Asz = 1,42 cm²/m.
3
Resultados
e discussões
O modelo simulado, que possui sua representação da interface aço-concreto
com os elementos de mola, combin39,
apresentou resultado que se aproxima do estudo experimental de Lawson et al. [6], como pode ser visto na Figura 7.
Os valores numéricos se mostraram mais próximos aos resultados obtidos na
análise experimental ao longo do trecho linear, e o momento fletor resistente
foi de 732,48 kNm, para um deslocamento de 143 mm. Desta forma, o resultado
final do momento fletor, ficou 7,28% inferior ao resultado de Lawson et al. [6].
Com a utilização dos elementos de contato targe173 e conta170,
os resultados numéricos ficaram próximos aos resultados experimentais, Figura 7,
obtendo o valor de 746,22 kNm para o momento fletor máximo, com uma flecha de
146 mm, apresentando desta forma, uma diferença de 5,54% do momento fletor
máximo resistido em relação ao estudo experimental de Lawson et al. [6].
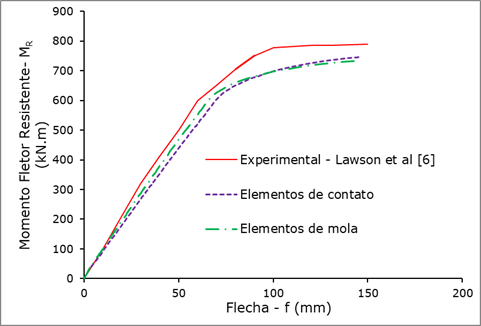
Figura
7. Diagrama de momento
fletor - flecha para interface com molas e interface com targe e conta.
A Figura 8 traz a distribuição de tensões no perfil metálico e na laje de concreto, para
o modelo em que foram utilizados os elementos de molas. Os resultados das
tensões encontradas nos referidos materiais ficaram praticamente equivalentes
nos dois modelos de interface apresentados, e dialogam com o resultado obtido
por Paes [7] em sua pesquisa. Isso demonstra que os modelos constitutivos
adotados para os materiais representam de forma satisfatória a estrutura. Na Figura 8 é
possível observar ainda que, para o nível de carregamento próximo à carga
máxima suportada pela viga, o perfil de aço se encontra plastificado na região
mais solicitada do modelo, que representa o centro da viga, com tensões normais
próximas ao valor do limite elástico do aço, de fy = 410 MPa.
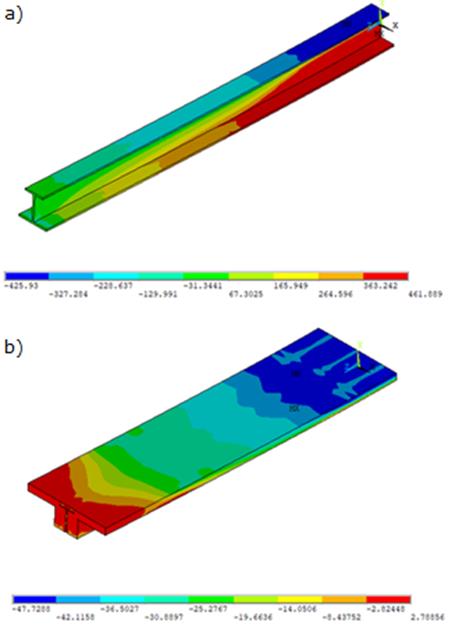
Figura
8. Distribuição de
tensões (MPa) no perfil metálico (a) e na laje de concreto (b).
É possível observar que na face superior da laje de concreto, regiões em
que se encontram aplicadas as forças que representam a atuação dos atuadores
hidráulicos, houve um acúmulo de tensões. Isso ocorre pelo fato de que, embora
as cargas tenham sido inseridas em vários nós e acrescidas ao modelo de forma
incremental, ocorreu um estado multiaxial de tensões nos elementos finitos.
Em relação às simulações de interface estudadas, ambas apresentaram
distribuições de deslizamentos verticais e longitudinais semelhantes. Como mostrado
na Figura 9,
a consideração da interface por elementos de mola leva a uma diferença entre os
deslocamentos entre o perfil metálico e a laje de concreto de aproximadamente
0,15 mm.
Para o modelo com os elementos de contato, a diferença entre o
deslocamento longitudinal no aço e no concreto foi de aproximadamente 1,00 mm, Figura 10.
Este fato pode ser justificado devido ao modelo composto por elementos de mola ter
maiores restrições de deslocamentos aplicadas ao longo da estrutura devido ao
acoplamento de deslocamentos nas direções ortogonais ao eixo longitudinal da
viga mista.
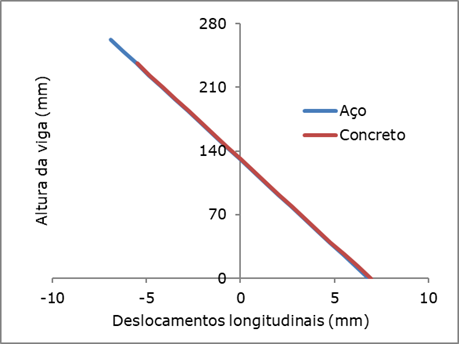
Figura
9. Deslocamentos
longitudinais do aço e do concreto, em relação ao eixo vertical, com elementos
de molas.
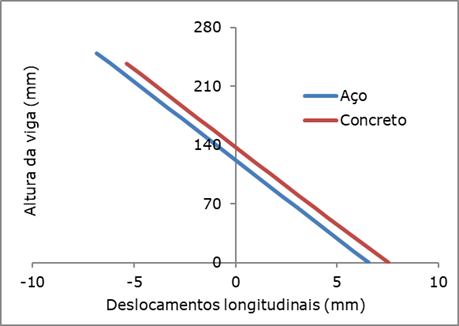
Figura
10. Gráfico dos
deslocamentos longitudinais do aço e do concreto, em relação ao eixo vertical,
com elementos de contato.
A diferença observada entre os resultados experimentais e numéricos na Figura 7 pode ser motivada pela dificuldade em representar as características do
concreto, como o módulo de elasticidade e demais coeficientes, de forma precisa.
Esta diferença também está associada com o aparecimento das primeiras fissuras
do concreto. Além disto, as armaduras foram simuladas sob a forma de taxas.
Desta forma, a distribuição de fissuras ocorre de maneira mais intensificada e
acelerada no modelo numérico, pois apesar das armaduras não impedirem a ruptura
do concreto, elas atuam também no sentido de controle da propagação de
fissuras.
O elemento que representa o concreto, solid65,
tem a capacidade de simular a fissuração do mesmo, em cada passo de carga
realizado (ANSYS [15]).
As fissuras podem ser sinalizadas através de três diferentes planos em cada
elemento. A primeira fissura no elemento é representada por um círculo
vermelho, a segunda por um círculo verde e a terceira por um círculo azul [15]. Se a fissura se fechar, é
representado um “x” dentro do círculo. Como pode ser visto na Figura 11, com aplicação equivalente a 10% do
carregamento total, é possível notar o aparecimento de algumas fissuras na
região onde ocorre a interação entre o aço e o concreto, concentradas no meio
do vão.
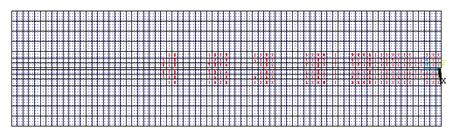
Figura
11. Vista superior da
viga com 10% do carregamento aplicado.
Na Figura 12 é possível observar o avanço da propagação das fissuras ao
longo de toda estrutura para 50% do carregamento aplicado, com aproximação nas
duas extremidades do modelo, sendo (a) que representa o extremo da viga, região
em que se encontra o apoio; e em (b) a região que representa o eixo central da
viga. É observada a partir desta imagem, uma propagação de fissuras na região
da capa superior da laje de concreto, proveniente da aplicação das cargas.
Finalmente, com a aplicação completa do carregamento, as fissuras se
encontram dispersas por praticamente toda a estrutura, como pode ser visto na Figura 13 com a vista frontal da laje de concreto. Nesta imagem é possível observar o
comportamento de fissuras que se abriram e posteriormente se fecharam
(representadas por x dentro do círculo), bem como as fissuras que se mantiveram
abertas (círculo sem preenchimento), e por fim, o surgimento de novas fissuras
representadas pelas cores verde (segunda fissura) e azul (terceira fissura).
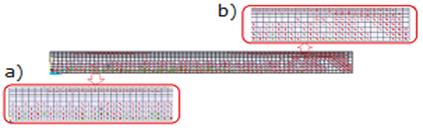
Figura
12. Vista lateral da laje
de concreto com 50% do carregamento total aplicado.
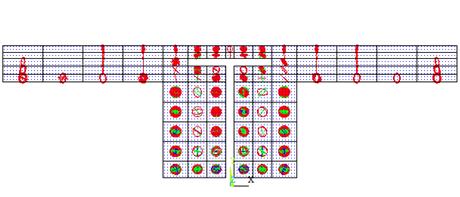
Figura
13. Vista frontal da laje
de concreto com o carregamento total aplicado.
4
Conclusões
Uma das principais dificuldades na simulação numérica de estruturas
mistas é a consideração da interface aço-concreto e da complexidade do
comportamento do concreto. Os resultados obtidos neste trabalho para a representação
da interação entre o aço e o concreto com elementos finitos de mola (COMBIN39)
e de contato (TARGE170 e CONTA173) aproximam-se do resultado experimental,
principalmente no trecho linear. Desta forma, obteve-se um modelo satisfatório para
a representação de pavimentos mistos de pequena altura. A comparação dos
resultados numéricos e experimentais apresentou dispersão entre 5 e 10%. Esta
diferença está associada principalmente à representação da fissuração do
concreto, que ocorre de maneira mais precoce no modelo numérico quando
comparada ao modelo experimental.
É possível supor que estas diferenças sejam ainda possivelmente
relacionadas à diferença das propriedades do concreto que se estima para o
modelo numérico, como a resistência a tração (fct) e o módulo de
elasticidade (Ec). Além disso, a representação da interface de
maneira aproximada e as condições para viabilizar a modelagem computacional,
como a condição de simetria, podem ser fatores que afetam a correlação entre os
resultados numéricos e experimentais. Além disso, a representação da malha
eletrosoldada através de elementos de barra de aço dispersos na laje de
concreto pode contribuir significativamente no controle de fissuras.
De forma geral o modelo mostrou-se capaz de representar de forma adequada
o complexo comportamento das vigas mistas de pequena altura, considerando duas
hipóteses para a simulação da interface aço-concreto, indicando sua viabilidade
para a utilização em pesquisas de estruturas mistas aço-concreto.
5
Referências
bibliográficas
[1] RAMOS, A. L. Análise numérica de pisos mistos aço-concreto de pequena
altura. 138 p. Dissertação (Mestrado em Engenharia de Estruturas). Escola de
Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 2011.
[2] MALITE, M. Análise do comportamento estrutural de vigas mistas
aço-concreto constituídas por perfis de chapa dobrada. 2v. Tese (Doutorado),
Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos,
1993. [2]
TAYLOR, H. F. W. Cement Chemistry, London: Thomas Telford, 2ed, 1997, 459 p.
[3] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8800. Projeto de
estruturas de aço e de estruturas mistas de aço e concreto de edifícios. Rio de
Janeiro: ABNT, 2008.
[4] KOCHEM, R. F. F. Modelagem numérica de piso misto de aço e concreto de
pequena altura: ênfase à ligação viga-pilar. 107 p. Dissertação (Mestrado em
Engenharia de Estruturas). Escola de Engenharia de São Carlos, Universidade de
São Paulo, São Carlos, 2018.
[5] HOU, Bingyu. Experimental and
Analytical Study of the Shear Transfer in Composite Shallow Cellular Floor
Beams. 2012. 316 f. Tese (Doutorado) - School of Engineering and Mathematical
Sciences, City University London, Londres, 2012.
[6] LAWSON, R. M.; MULLETT, D. L.;
RACKHAM, J. W. Design of Asymmetric Slimflor Beams Using Deep Composite
Decking. SCI Publication P175. The Steel Construction Institute, 1997.
[7] PAES, José Luiz Rangel. Aportaciones al Análisis del
Comportamiento Estructural de Sistemas Forjados Mixtos Tipo "Slim Floor".
2003. 403 f. Tese (Doutorado) – Programa de Doctorat d’Enginyeria de la
Construcció, Universitat Politècnica de Catalunya, Barcelona, Espanha, 2003.
[8] LESKELÄ, M. V.; HOPIA, J. Steel
Sections for Composite Shallow Floors. Report RLT 0053E. University of Oulu,
Structural Engineering Laboratory. Finlandia, 2000.
[9] LAM, D.; DAI, X.; KUHLMANN, U.;
RAICHLE, J.; BRAUN, M. Slim-floor construction – design for ultimate limit
state. Steel Construction 8. n. 2. Berlim. 2015.
[10] CHEN, S.; LIMAZIE, T. Composite Slim
Floor beams with innovative shear connections. Report RLT 0053E.
Proceedings of the ICE – Structures and Buildings. Londres, 2018.
[11] Sheehan, T; Dai, X.; Yang, J; Zhou, K; Lam, D. Flexural behaviour of composite Slim
Floor beams. Structure, 21, p. 22-32, 2019.
[12] SCHORR, J., KUHLMANN, U. Design of Slim
Flors and their connections between steel and concrete. The 14th
Nordic Steel Construction Conference, 2019.
[13] BALDASSINO, N., ROVERSO, G., RANZI,
G., ZANDONINI, R. Service and ultimate bahaviour of Slim Floor beam: na
experimental study. Structures, 17, p. 74-86, 2019.
[14] ROCHA, F.M., MUNAIAR NETO, J.
Analysis of Slim Floor beams infire: emphasis on the concrete
constitutive models. Revista IBRACON de Estruturas e Materiais, 7 n 1, p.
158-177, 2014.
[15] ANSYS. User´s Manual for revision 11. Swanson
Analysis Systems Inc. Inc., Houston, PA, 2010.
[16] MARCONCIN, L. R. Modelagem numérica de vigas mistas de aço-concreto.
Dissertação (Mestrado em Construção Civil) Universidade Federal do Paraná,
Curitiba, 2008.
[17] KOTINDA, T. I. Modelagem numérica de vigas mistas aço-concreto
simplesmente apoiadas: ênfase ao estudo da interface laje-viga. 120 p.
Dissertação (Mestrado em Engenharia de Estruturas). Escola de Engenharia de São
Carlos, Universidade de São Paulo, São Carlos, 2006.
[18] OLIVEIRA, J. P. S.; DIAS J. V. F.; FAKURY, R. H.; CALEZANI A. F. G.
Análise numérica da flambagem lateral com distorção em vigas mistas de
aço-concreto. CILAMCE 2017.
[19] MODEL CODE 2010. Final draft.
Fédération Internacionale du Béton (FIB). Vol. 1. 2012.
orcid.org/0000-0003-3261-9089
orcid.org/0000-0002-3787-5535
orcid.org/0000-0002-4213-7473