1
Introdução
Atualmente,
devido ao crescimento populacional e ao aumento do consumo de energia, que
levam ao esgotamento gradual dos combustíveis fósseis convencionais, estudos
sobre novas formas de produção de energia é linha de pesquisa para vários
cientistas [1]. A energia solar que é limpa e
renovável é abundante e generalizada para atender à demanda por combustíveis de
forma ambientalmente amigável e sustentável [2]. Um método de utilização desta energia solar é a
conversão da radiação solar em energia para a obtenção de combustíveis químicos,
e o hidrogênio, que é um combustível alternativo, pode ser produzido por
radiação solar em um reator termoquímico solar. No entanto, o projeto destes
reatores e seu desempenho térmico são fatores relevantes que têm um impacto
significativo na eficiência da produção e precisam ser investigados.
Existem vários
estudos sobre a importância da transferência de calor no reator termoquímico
solar. Wang et al. [3] estudaram
que a distribuição da irradiação solar concentrada tem um impacto significativo
na distribuição de temperatura do receptor de meio poroso. Os autores
combinaram os métodos de rastreamento de raios de Monte Carlo e o Software Fluent
com as funções definidas pelo usuário para investir o desempenho térmico do
receptor de meio poroso, desta forma as influências típicas da condição de
limite do fluxo de calor, perda de calor de radiação, porosidade, emissividade,
massa de fluxo e o diâmetro médio de partículas nas distribuições de
temperatura foram calculadas ao longo do receptor. Paal et al. [4] desenvolveram uma abordagem de
transferência de calor analítica para receptor de mídia volumétrico poroso, que
levou em consideração a distribuição de irradiação tridimensional e sua
influência sobre o fluxo de fluidos. Os resultados numéricos mostram que as
distribuições de temperatura do receptor de mídia poroso volumétrico são
fortemente influenciadas pela distribuição de radiação solar. Zhang et al. [5] estudaram as características de
transporte térmico e o fluxo de fluidos em reatores termoquímicos solares de
mídia porosa de alta temperatura, eles investigaram com diferentes modelos
termo-físicos usando funções definidas pelo software FLUENT. Os resultados indicaram
que o modelo local de não-equilíbrio térmico e o modelo de transferência
radiativa são indispensáveis para a análise de desempenho térmico do sistema de
reação termoquímico de alta temperatura de trabalho. No entanto, o cálculo da
radiação solar pode ser calculado por diferentes métodos, e há muitas dúvidas
sobre a melhor maneira de simular a radiação e como analisar o efeito da
temperatura em um reator termoquímico solar.
Além disso, a
maioria das pesquisas foram investigadas experimental e numericamente para
produzir H2 em alta temperatura, superior a 700K, sem fonte solar [6]. O principal foco dos estudos
experimentais foi desenvolver os catalisadores robustos que serão resistentes à
deposição de carbono. Por um lado, os reatores convencionais industriais são
operados entre 808 e 3535 kPa e 1073 a 1273 K, mas o processo de equilíbrio
limitado pode chegar a uma conversão do componente de cerca de 93%. Neste
sentido, o uso de reatores de membrana tem sido amplamente pesquisado, devido à
facilidade de produção e ao conceito de "intensificação do processo",
ou seja, produção e separação no mesmo equipamento por meio de membranas
seletivas. As aplicações de reatores de membrana oferecem uma possível forma
para superar a baixa conversão, removendo seletivamente o hidrogênio de um
sistema seletivo de membrana, resultando em maiores conversões de metanol em
temperaturas mais baixas. As membranas mais comumente usadas para remover
hidrogênio são membranas de paládio densas ou membranas de paládio. Estas
membranas oferecem alta seletividade sobre outros gases por causa da dissolução
seletiva de átomos de hidrogênio na matriz metálica.
Neste sentido,
a modelagem matemática e a solução numérica são usadas para obter uma melhor representação
dos fenômenos no reator termoquímico solar (STR) através da consideração de
turbulência, calor e transferências em massa, reações químicas, bem como a
fenomenologia do reator. Os modelos matemáticos são úteis para investigar os
efeitos das condições operacionais primárias, otimização e ampliação no STR. O
desempenho dos STRs pode ser investigado além da faixa de parâmetros já estudadas
experimentalmente devido às limitações impostas por considerações econômicas e
de segurança [6]. Os
parâmetros físicos e químicos são acoplados pelos fenômenos de transferência de
calor e massa presentes no reator [7].
Portanto, para
estudar a análise térmica do desempenho de um reator termoquímico solar e a
conversão do tolueno, este trabalho apresenta a modelagem numérica da
transferência de calor e massa em um reator termoquímico solar com a radiação
solar calculada pela aproximação de Rosseland. Assim, com base na transferência
de calor e massa, um sistema de equações diferenciais parciais (EDP) foi
formulado para descrever equações de governo do balanço de massa e energia.
Aplicando a metodologia da Diferença Finita (FD) foi possível transformar o PDE
em Equações Diferenciais Ordinárias (EDO), e com o comando NDSolve em software
Mathematica. Assim, foram obtidos os gráficos das temperaturas, análises de
sensibilidade de parâmetros, o valor da radiação solar e a conversão do metanol.
2
Formulação
do Problema
Nas
últimas duas décadas, pesquisas provaram o uso eficiente da energia solar
térmica para impulsionar reações de reforma altamente endotérmicas. Para este
fim, uma configuração esquemática (ver Fig. 1) foi empregada para estudar a
transferência de calor. Fig. 1 mostra o esquema simplificado de um reator
termoquímico solar que é usado como geometria de domínio computacional para a
simulação numérica. É possível perceber pela figura que a transferência de
calor que ocorrerá no reator será influenciada pela irradiação solar
concentrada que atuará diretamente na região porosa.
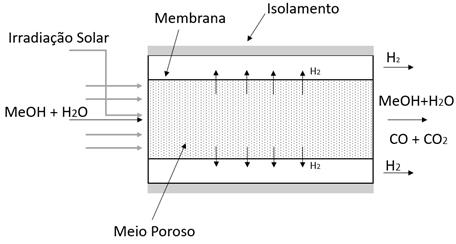
Figura 1. Modelo simplificado de reator termoquímico solar com membrana.
2.1
Modelo
Matemático
O objetivo principal desta seção é o
desenvolvimento de um modelo matemático robusto que será capaz de simular o
comportamento da transferência de calor e massa no STR.
A equação de
balanço de massa no lado do tubo é expressa levando em consideração a difusão
na direção radial e a transferência de massa convectiva na direção axial. Os
parâmetros e equações presentes na modelagem podem ser encontrados na
referência [13].
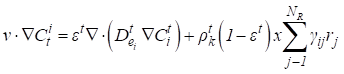 (1)
(1)
- Condições de
contorno:
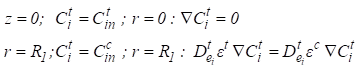 (2)
(2)
Para o balanço de energia, as seguintes
considerações foram adotadas: (i) fase ideal de gás, (ii) dispersão axial
dentro do STR, (iii) sem fenômenos de difusão de componentes químicos na
superfície catalisadora e dentro do catalisador ocorrem, (iv) pressão STR
constante (sem queda de pressão no STR) e velocidade superficial constante, (v)
STR opera em regime estacionário, (vi) porosidade na direção axial do STR foi considerada
constante, (vii) propriedades físicas constantes (densidade, peso catalisador,
tamanhos de partículas uniformes) sobre a gama de condições operacionais a
partir de STR, respectivamente. Mais detalhes sobre a transferência de calor em
meios podem ser observados em Ref. [14] Com base nas suposições acima, a equação energética (dentro do
STR) é formulada da seguinte forma.
- Balanço de Energia
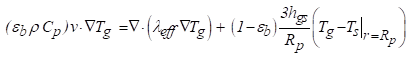 (3)
(3)
No Eq. 1, r (kg/m3) é
a densidade da mistura gasosa, Tg (K) é a temperatura da fase
gasosa,Cp (kJ/kg K) é a capacidade de calor molar em pressão
constante da mistura gasosa, hgs (W/m2 K) coeficiente de
transferência de calor de convecção volumétrico entre a fase fluida e a fase
sólida, eb (-) é a fração de
vazio do leito, rp (m) é o raio de partículas, Ts (K) é
a temperatura da fase sólida, respectivamente.
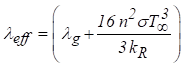 (4)
(4)
Onde,
l g (W/m
K) é a condutividade térmica a gás, n (-) é o índice refrativo, s
(W/m2 T4) é a constante de Stefan-Boltzmann, T¥
(K) é a temperatura ambiente, kR (m-1) é o coeficiente de extinção
de Rosseland em meio poroso, respectivamente,
O símbolo hgs é
o coeficiente de transferência de calor de
convecção volumétrica entre a fase fluida e a fase sólida. A correlação
empírica proposta por Wu et al. [8] é usado:
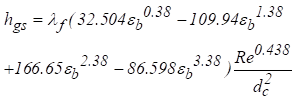 (5)
(5)
Essa correlação é válida para 0.66< 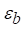 < 0. 93 e 70
< Re < 800
< 0. 93 e 70
< Re < 800
As condições iniciais e de
limite adequadas de Eq. (1) são dadas da seguinte forma:
Na entrada:
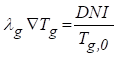 (6)
(6)
Onde
o DNI é a Irradiação Normal Direta (W/m²) e OT g.0 é a temperatura
inicial da fase gasosa.
Na
saída:
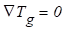 (7)
(7)
2.2
Radiação
Solar
Entre os
fenômenos térmicos que podem ocorrer em um reator termoquímico solar, o termo
de radiação é considerado o mais complexo quando comparado à convecção e
condução. Desta forma, o seu estudo recebe um destaque. Uma vez que o meio
poroso absorve fortemente a radiação solar, é de alta espessura óptica e
apresenta um caminho médio de transporte de radiação curto. Para obter o termo
fonte de radiação, a Equação de Transferência Radiativa (RTE) precisa ser
resolvida [9]:
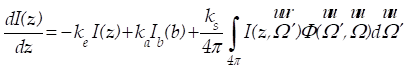 (8)
(8)
Onde o símbolo
“i” é a intensidade de radiação local no meio poroso que varia de acordo com o
espaço (z) e a direção (Ω), a função de fase Φ varia de direção. O símbolo Ke é
o coeficiente de extinção do receptor solar da mídia porosa, Ka é o coeficiente
de absorção, e Ks é o coeficiente de dispersão.
Para resolver
o ETR a aproximação de Rosseland é uma das melhores opções, porque este método
é usado para problemas de espessura óptica considerável e não consome tempo
devido à simplicidade e pode fornecer previsões razoavelmente boas em
comparação com medidas experimentais para estudar os mecanismos de
transferência radiativa em meios de comunicação porosos [10].
2.3
Aproximação
de Rosseland
Através da aproximação de Rosseland, o RTE pode ser
simplificado como [11].
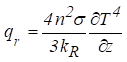 (9)
(9)
Foi considerado que as diferenças de temperatura dentro do fluxo são tais
que o termo T4 pode ser expresso como uma função linear da
temperatura. Isso é conseguido expandindo o T4 em uma série de
Taylor sobre t1 e negligenciando a ordem superior.
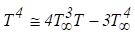 (10)
(10)
Assim, o problema de transferência de calor radiativo é reduzido para ser
um problema de condução simples com condutividade fortemente dependente de
temperatura, da seguinte forma.
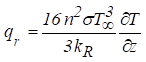 (11)
(11)
O coeficiente de extinção (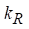 ) é
avaliado como a soma da absorção (
) é
avaliado como a soma da absorção (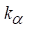 ) e coeficientes de dispersão (
) e coeficientes de dispersão (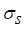 )
da seguinte forma
)
da seguinte forma
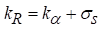 (12)
(12)
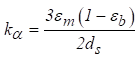 (13)
(13)
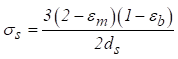 (14)
(14)
Onde, 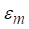 é
a porosidade do reator,
é
a porosidade do reator, 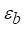 é a
porosidade da cama, e ds é o diâmetro da cama.
é a
porosidade da cama, e ds é o diâmetro da cama.
2.4
Reformar
a Vapor do Metanol
A reação de reforma a vapor do metanol é
vista como muito atraente e promissora para produção de hidrogênio de acordo
com a literatura científica e pode ser descrita pelas seguintes reações
químicas:
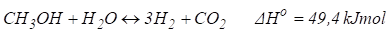 (15)
(15)
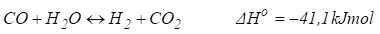 (16)
(16)
 (17)
(17)
Onde, a reação (15) se refere a reforma a
vapor do metanol (RVM), (16) a reação de decomposição (RD) e a (16) é a reação
do deslocamento gás-água (RDGA). Deve-se notar que, algebricamente a reação (15)
é a soma das outras duas reações.
Nesse estudo, a análise cinética para o
processo de reforma a vapor do metanol é desenvolvida baseada no modelo
proposto por Peppley [12]. No desenvolvimento do modelo cinético, é suposto que os sítios
ativos para a reação de decomposição são diferentes daqueles para as reações de
reforma a vapor do metanol, deslocamento gás-água, hidrogênio e as espécies
contendo oxigênio absorvem sobre diferentes sítios ativos. Baseada no modelo de
Langmuir-Hinshelwood as taxas das três reações são expressas como:
- Expressão para Taxa de Reação para a
Reforma à Vapor do Metanol.
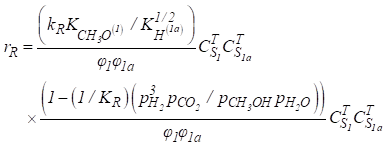 (18)
(18)
- Expressão para Taxa de Reação de
deslocamento gás-água.
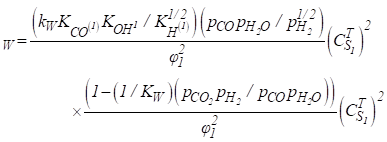 (19)
(19)
- Expressão para Taxa de Reação de
decomposição do metanol.
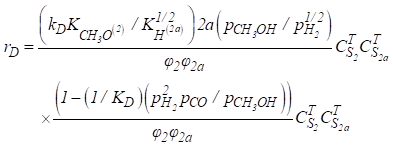 (20)
(20)
Onde, 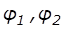 e
e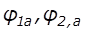 são
denominados como o termo de absorção para cada reação e
são
denominados como o termo de absorção para cada reação e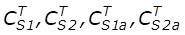 são a
concentração total da superfície do catalizador.
são a
concentração total da superfície do catalizador.
Onde, kj para (j = R, D, W) representa a
taxa para as diferentes reações (Eqs. 11-13) e Kj para (j = R, D, W) são as
constantes de equilíbrio para as diferentes reações
As constantes de equilíbrio Kj para (j = CH3O(1),
HCOO(1), OH(1), CO2(1), H(1a), CH3O(2),
HCOO(2), OH(2), CO2(2), H(2a)) de
cada componente presente na Ref. [13].
3
Metodologia
de Solução
Para resolver as equações propostas, foi
adotado o Método da Diferença Finita (DF). A DF é um método tradicional de
resolução de equações diferenciais que se baseiam na aproximação de derivados
por diferenças finitas. A fórmula de aproximação foi obtida da série Taylor da
função derivada. As definições abaixo, Eq. (13 - 16), foram utilizadas com as
respectivas condições de limite de cada elemento. Após a aplicação do DFM e
através do software Mathematica e comando NDSolve foi possível obteve os
resultados deste trabalho. Para ilustrar o MDF, Fig. 2 mostra uma abordagem
simplificada para os pontos da malha escolhida.
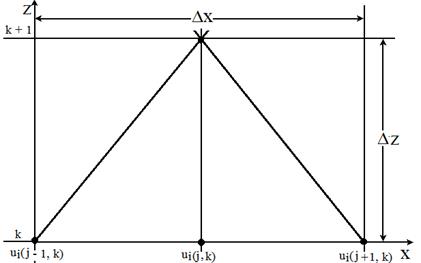
Figura 2. A malha aponta para uma solução numérica
usando o método da diferença finita.
A relação abaixo foi utilizada na equação geral do
problema e da condição de contorno, permitindo a discretização e a obtenção dos
EDOs para cálculo em Mathematica.
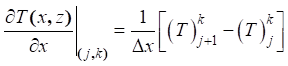 (21)
(21)
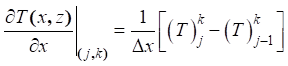 (22)
(22)
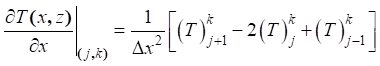 (23)
(23)
4 Resultados
Um
algoritmo computacional na plataforma Mathematica a sub-rotina Solve foi
elaborado pelos autores para resolver as equações do modelo mencionadas neste
trabalho. Portanto, as condições operacionais, parâmetros energéticos para
simular as variáveis do processo SRT são apresentadas na Tabela 1. Neste
estudo, o modelo matemático foi confirmado através da distribuição de
temperatura no SRT. Fig. 3 mostra o perfil de temperatura obtido por Lougou et
al. [1], e a simulação numérica do
presente estudo. A comparação mostra um bom ajuste entre os resultados deste
trabalho com a literatura, e ambos seguem um comportamento semelhante.
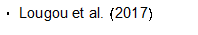

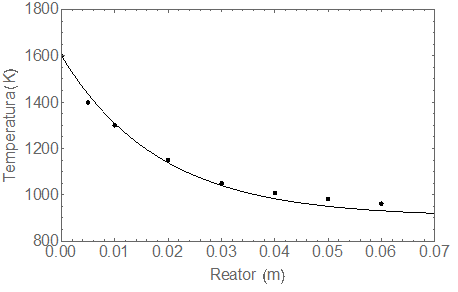
Figura 3. Variação
de temperatura em um reator termoquímico solar, e comparação com resultados
encontrados na literatura.
Tabela 1. Condições operacionais, parâmetros
cinéticos e parâmetros de massa.
|
Categorias
|
Propriedades
|
Valores
numéricos
|
|
Condições
de operação
|
Pressão
operacional
Temperatura
operacional
Taxa
de fluxo de gás
Fração
de vazio da cama
Emissividade da mídia porosa
Diâmetro
do reator
Comprimento
do reator
|
1.01
1800
3.5x10-5
0.77
0.92
0.032
0.14
|
|
Parâmetros
térmicos
|
A densidade da
mistura gasosa
A capacidade de calor molar
Diâmetro
STR
Condutividade térmica a gás
Stefan-Boltzmann
constante
Coef.
trans. de calor gás-sólido
Temperatura
ambiente
Coeficiente
de Rosseland
|
0.693
1.079
0.32
109.123
2.67x10-8
13.3x10²;
300
1.738x104
|
A figura 4 mostra o perfil da distribuição de
temperatura do reator com 14 cm. Como indicado em Fig. 4, a cavidade interna do
reator é mais aquecida quando as intensidades difusas de irradiação solar foram
aumentadas de 80 para 100 kW/m². A temperatura mais alta observada na região
frontal do reator é evidente devido ao maior fluxo de calor radiativo emitido
porque a irradiação solar é difundida diretamente nesta parte Ref. [1]. Os altos valores de temperatura e a
distribuição de fluxo de calor de radiação obtidos poderiam fornecer a energia
térmica necessária para a realização da reação química para produzir hidrogênio
ou gás de síntese.

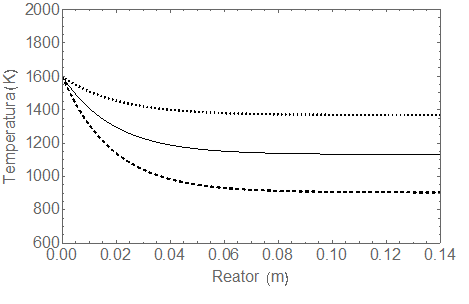
Figura 4.
Perfil da temperatura em três valores em intensidades difusas da irradiação
solar.
A figura 5 mostra o fluxo de calor da radiação ao longo
do sentido do fluxo do reator. O parâmetro de porosidade tem uma forte
influência sobre o coeficiente de extinção e o coeficiente de transferência de
calor do reator termoquímico solar. Para analisar isso, os efeitos da porosidade
na distribuição do fluxo de calor radiação foram traçados em Fig. 5. Três
porosidades, 0. 7,0. 8,0. 9, foram investigados. Como se observa, o fluxo de
calor da radiação aumenta com o aumento da porosidade, portanto, foi obtida a
temperatura máxima com o valor mais alto da porosidade. O Fluxo de Calor de
Radiação inicial com aproximadamente 9100 W/m², 7200 W/m² e 6100 W/m² e com sua
respectiva porosidade, 0. 90,0. 80 e 0,40 estabiliza com 5800 W/m², 4200 W/m² e
3400 W/m². A espessura da região térmica não-equilíbrio aumenta lentamente com
o aumento da porosidade.
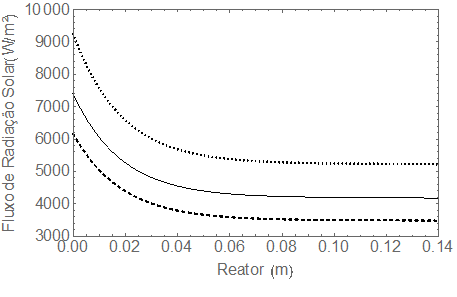
Figura 5. Perfil do fluxo de calor de radiação em
diferentes condições de porosidade.
A
conversão do metanol é calculada a partir das concentrações obtidas pelo
balanço de massa e pela diferença da razão dos componentes iniciais pela razão do
componente calculado com os iniciais. Utilizando esta metodologia, a conversão
do metanol é apresentada na Fig. 6, é notado que praticamente 90% do metanol
foi convertido, sendo este transformado em gás de síntese ou hidrogênio.
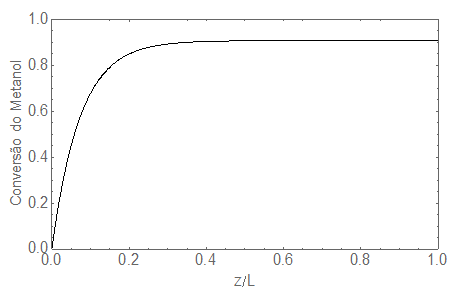
Figura 6.
Conversão do Metanol em um Reator Termoquímico Solar.
A Fig. 7 apresenta a produção de
hidrogênio no reator termoquímico solar. Esta produção é calculada com relação
da razão quantidade de concentração de hidrogênio calculada, pela concentração
de metanol de entrada. A produção de hidrogênio alcançou um valor de 2.5 a
quantidade inicial de metanol. Desta forma, pode-se concluir que o RTS, é um
equipamento aconselhável para produzir energia renovável e pesquisa sobre
formas de armazenamento e utilização desse hidrogênio devem ser realizadas.
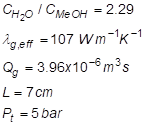
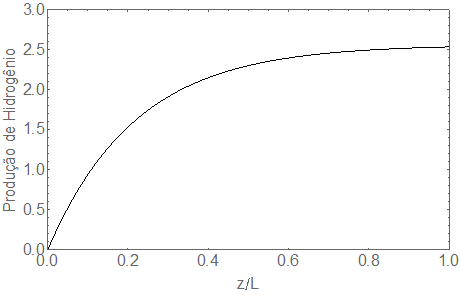
Figura 7.
Produção de Hidrogênio em um Reator Termoquímico Solar.
5 Conclusão
O desempenho térmico e a conversão do metanol em um
reator termoquímico solar para a produção de gás de síntese foram investigados.
Esta pesquisa foi realizada numericamente através do método de diferença
finita, e comando NDSolve no Mathematica e o modelo foi validado com os
resultados disponíveis na literatura (Lougou et al. 2017). A diferença finita
foi usada para transformar os EDPs em EDOs e com NDSolve foram obtidos os
perfis da temperatura, da radiação do reator termoquímico solar, conversão do
metanol, e produção de hidrogênio. As seguintes
conclusões foram tiradas:
(i)
A
perda de calor de radiação na superfície do reator não pode ser negligenciada
durante a análise de desempenho térmico do receptor de mídia poroso.
(ii)
O
fluxo máximo de calor de radiação aumenta com o aumento da porosidade.
(iii)
A
cavidade interna do reator é mais aquecida quando a irradiação solar difusa foi
aumentada de 80 para 100 kW/m².
(iv)
90%
do metanol foi convertido, sendo utilizado para produção de hidrogênio. A
produção de hidrogênio em um RTS, alcançou 2.5 vezes em relação a quantidade
inicial de metanol.
Referências
[1] LOUGOU, B. G., SHUAI, Y., XING, H.,
YUAN, Y. AND TAN, H., 2017. Thermal performance analysis of a solar
thermochemical reactor for syngas production. International Journal of Heat
and Mass Transfer, v.111, p. 410-418, 2017.
[2] WANG H., LIU M., KONG H. AND HAO, Y..
Thermodynamic Analysis on Mid/low-Temperature Solar Methane Steam Reforming
with Hydrogen Permeation Membrane Reactors. Applied Thermal Engineering.
v.152, p. 925-936, 2019.
[3]
WANG, F., SHUAI, Y., TAN, H, AND YU, C. Thermal performance analysis of porous
media receiver with concentrated solar irradiation. International Journal
of Heat and Mass Transfer. v. 62, p. 247-254, 2013.
[4] PAAL, R.P., HOFFSCHMIDT, B., BÖHMER,
M., AND BECKER, M. Experimental and numerical evaluation of the performance and
flow stability of different types of open volumetric absorber under
non-homogeneous irradiation. J. Sol. Energy Eng. v. 60, p.
135–150, 1997.
[5] ZHANG, H., LOUGOU, B., PAN, R.,
SHUAI, Y. WANG, F., CHEN, Z., TAN, H. Analysis of thermal transport and fluid
flow in high-temperature porous media solar thermochemical reactor. Solar Energy, v. 173, p. 814-824, 2018.
[6] ANJOS, E., DAMASCENO, J., OLIVEIRA, C., SILVA, A., SILVA, J. Numerical Analysis of the
steam reforming of toluene to produce hydrogen in a fixed bed catalytic
reactor. In Proceedings of the 17th Brazilian Congress of Thermal Sciences and
Engineering – ENCIT 2018. Águas de Lindoia - SP, Brazil,
2018.
[7]
ANJOS, E., OLIVEIRA, C., SILVA, J. Dynamic analysis to
produce hydrogen in a fixed bed catalytic reactor by the steam reforming of
toluene. Chemical Engineering Transaction. v.74, p. 553-558, 2019.
[8] WU, Z., CALIOT, C., FLAMANT, G., WANG,
Z. Numerical simulation of convective heat transfer between airflow and ceramic
foams to optimize volumetric solar air receiver performances. Int. J. of
Heat and Mass Transfer. v.54, p.1527-1537, 2011.
[9] WANG, F., MAN, L., CHENG,
Z., TAN, J. HUANG, LINHU, X. L. Radiative heat transfer in solar thermochemical
particle reactor: A comprehensive review. Renewable and Sustainable
Energy Reviews. v. 73, p. 935-949, 2017.
[10] KODAMA, T., GOKON, N.
“Thermochemical cycles for high-temperature solar hydrogen production.” Chem.
Rev. v. 107, p. 4048–4077, 2007.
[11] MAGYARI, E., PANTOKRATORAS,
A. Note on the effect of thermal radiation in the linearized Rosseland
approximation on the heat transfer characteristics of various boundary layer
flows. International Communications in Heat and Mass Transfer. v. 38, p.
554-556, 2011.
[12] PEPPLEY, B. A. Methanol
steam reforming on Cu/ZnO/Al2O3 catalysts. Part 2. A comprehensive kinetic
model. Applied Catalysis A: General. v.179, p. 31-49, 1999.
[13] SAIDI., M.
Performance assessment and evaluation of catalytic membrane reactor for pure
hydrogen production via steam reforming of methanol. International Journal
of Hydrogen Energy, v. 42, p. 16170-16185, 2017.
[14] NIELD, D., BEJAN, A. Convection in porous media. New
York: springer, 2006.
orcid.org/0000-0001-5727-2427
orcid.org/0000-0001-5727-2427