1
Introdução
É
usual nos estudos das redes aéreas de distribuição (RAD) considerar o aterramento
a partir de um valor constante de resistência, que representa o comportamento
elétrico da malha ou eletrodo de aterramento no ponto de injeção da corrente de
falha para o solo.
No
entanto, essa representação simplificada do aterramento na condição de descarga
atmosférica pode apresentar resultados equivocados. Para uma abordagem mais
realista, esse parâmetro deveria ser referido como uma resistência transitória,
capaz de representar melhor a resposta do sistema na presença de ocorrências
associadas com fenômenos rápidos e de alta intensidade. Deste modo, as
práticas convencionais de aterramento, que são consistentes para condições de
baixa frequência (ex. falhas oriundas de curto-circuito), podem não ter sentido
quando o sistema é submetido à ação de descargas atmosféricas, devido ao fato
do comportamento eletromagnético do aterramento nessas condições ser muito mais
complexo.
Sabe-se
que as altas magnitudes das correntes produzidas pelas descargas atmosféricas
que escoam através do aterramento, desencadeiam um processo de ionização do
solo no entorno dos condutores devido aos elevados valores de campo elétrico
induzidos, levando à ruptura dielétrica do solo. Esse fenômeno altera
consideravelmente o comportamento da resistividade do solo e, consequentemente,
provoca uma variação transitória significativa da resistência de aterramento do
eletrodo [1 – 4].
Portanto,
no intuito de se obter resultados mais confiáveis, alguns modelos matemáticos
têm sido desenvolvidos para considerar a ionização do solo e o comportamento
transitório da resistência na modelagem dos sistemas de aterramento. O mais
simples e conhecido de todos é o modelo Geométrico, desenvolvido por um grupo
de trabalho do CIGRE (International Council on Large Electric System) [5, 6]. Este método é principalmente aplicado em
estudos de linhas de transmissão de energia de alta tensão [7].
Um
outro modelo recorrente na literatura acadêmica é o conhecido como Dinâmico.
Este modelo se caracteriza por realizar uma abordagem mais física do fenômeno
de ionização, pois considera a variação do parâmetro da resistividade elétrica
do solo na região ionizada [8, 9].
A
maioria dos estudos que utilizam o modelo Dinâmico são focados na análise
isolada da topologia de aterramento, sem interação com as outras estruturas do
sistema elétrico. A implementação é efetuada a partir de técnicas de modelagem
numérica, em especial o método FDTD [10, 11]. Esta ferramenta computacional, apesar da
sua robustez e de proporcionar resultados altamente precisos, demanda um
esforço computacional considerável, podendo um problema de dimensões
geométricas relativamente pequenas levar vários dias de execução da simulação.
Neste
contexto, será apresentado no artigo uma proposta de incorporação das
formulações analíticas dos modelos da ionização do solo (Geométrico e
Dinâmico), em uma plataforma para o cálculo de transitórios eletromagnéticos,
no caso o programa ATP Draw® (Alternative Transient Program).
Assim,
a partir de simulações que demandam baixo tempo de processamento, poderá ser
avaliada a influência do aterramento ionizado nas demais estruturas componentes
da rede de distribuição. Isto permitirá fazer uma análise mais realista dos
processos transitórios que ocorrem na rede – originários dos efeitos das
descargas atmosféricas – em relação aos casos em que os modelos tradicionais de
resistência de aterramento invariável no tempo são empregados.
A
revisão bibliográfica realizada pelos autores deste trabalho constatou que
poucas publicações abordam a temática de simulação ATP de redes de distribuição
considerando a ionização do solo nos aterramentos elétricos. Por exemplo, Mata et
al [12] fizeram a modelagem ATP de uma rede aérea de
distribuição experimental a dois condutores, sendo o aterramento representado
pelo modelo Geométrico. Já Gondim et al [13] implementaram
no ATP o modelo Dinâmico, como parte de um estudo de qualidade de energia e
análise de danos em equipamentos elétricos de baixa tensão.
Mais
especificamente, neste artigo será mostrado um estudo comparativo do
comportamento dos níveis de sobretensão nas fases do lado primário (média
tensão) e no cabo mensageiro ou guarda de uma RAD do tipo compacta na situação
de descarga direta. As simulações ATP irão considerar os dois modelos de
ionização do aterramento (Geométrico e Dinâmico) e a representação convencional
aplicada pelas concessionárias (resistência de valor constante).
2
Referencial
teórico
2.1
Aterramento
elétrico em RAD
As
malhas de aterramento empregadas nas RAD são geralmente de pequenas dimensões,
devido aos custos envolvidos e às restrições impostas pelas limitações de
espaço físico para sua instalação. Tipicamente, as topologias consistem em
hastes cilíndricas condutoras enterradas verticalmente no solo, alinhadas e
interligadas. Em geral, as hastes são de aço cobreado com 2,4 metros de
comprimento, 16 mm de diâmetro e espaçadas a 3 metros (no caso do uso de mais
de uma haste), enterradas a uma profundidade mínima de 30 centímetros.
O
cabo neutro do lado de baixa tensão da rede e o cabo de guarda (no caso
específico das redes do tipo compactas), devem estar aterrados no máximo a cada
200 metros, aproximadamente. Ainda, todas as massas dos equipamentos de média
tensão instalados nos postes (ex. transformadores), assim como os finais de linha
e para-raios, devem também obrigatoriamente estar aterrados. O aterramento é
executado no solo na proximidade da base dos postes, estando ligado pelo cabo
de descida às estruturas da rede localizadas no topo.
Para o cálculo
analítico da resistência de aterramento de uma haste vertical simples, é usual
aplicar a expressão clássica de Sunde [14],
|
|
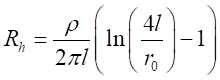
|
(1)
|
onde: Rh (Ω) é
a resistência de aterramento da haste vertical; 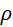 (Ω∙m) é a resistividade elétrica
aparente do solo; r0 e l, em metros, são o raio da
seção transversal e o comprimento da haste, respectivamente.
(Ω∙m) é a resistividade elétrica
aparente do solo; r0 e l, em metros, são o raio da
seção transversal e o comprimento da haste, respectivamente.
A utilização
na expressão (1) da resistividade aparente vista pelo aterramento em integração
com o solo, no lugar de simplesmente uma resistividade uniforme (por exemplo,
aquela da camada superficial do solo), contribui para uma modelagem mais
precisa. Este parâmetro considera a profundidade
atingida pelo escoamento das correntes elétricas e a não homogeneidade do solo, pois para sua
obtenção é levado em consideração a estratificação do solo em camadas
horizontais [15].
No
caso do uso de várias hastes verticais interligadas, para obter a resistência
equivalente do conjunto é aplicado um fator de redução à Equação (1). Este
coeficiente depende da quantidade de hastes e da separação entre elas. Por
exemplo, para a configuração mais empregada nos aterramentos de RAD, que é a
topologia de três hastes com espaçamento regular de 3 metros, o fator de
redução a ser aplicado é igual a 0,397 [15]. Assim,
para representar os eletrodos de aterramento na modelagem de RAD o uso de
expressão (1) ou outras equivalentes, que fornecem um valor constante de
resistência, é suficientemente preciso nas situações em que as correntes de
falha que circulam pelo aterramento não apresentarem níveis muito elevados.
Isto acontece, por exemplo, nos casos de curtos-circuitos fase-terra à frequência
industrial (50/60 Hz). Já na condição de descarga atmosférica, os surtos de
corrente podem atingir picos da ordem de dezenas e até centenas de kiloampères [16], capazes de provocarem a ionização do solo.
Nestas condições, a resistência do aterramento irá apresentar um comportamento
dinâmico, que não é contemplado pelos modelos convencionais.
2.2
Fenômeno
da ionização do solo
Se
a amplitude da corrente de surto oriunda da descarga atmosférica que atinge o
aterramento é muito alta, um processo de ionização pode ocorrer no solo no
entorno do eletrodo de injeção, devido aos elevados valores de campos elétricos
associados.
Quando
o gradiente do potencial elétrico no solo excede um determinado patamar
crítico, ocorre um processo disruptivo no solo. Este valor de campo elétrico
crítico depende do tipo de solo (caraterizado pela resistividade elétrica) e da
condição de umidade. Valores relatados na literatura compreendem uma faixa de
300 a 1.100 kV/m [5, 17]. Para
quantificar este parâmetro, Oettle [18] propôs o emprego de uma expressão em que o
campo crítico é função da resistividade do solo na condição de pré ionização,
isto é,
|
|
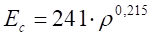
|
(2)
|
em que Ec
(kV/m), é o campo elétrico crítico e ρ (Ω∙m) representa a resistividade
elétrica inicial do solo. Na medida que a intensidade da corrente que flui pelo
solo aumenta, streamers são gerados e evaporam a umidade. Como
consequência, arcos elétricos são produzidos ao redor do eletrodo de
aterramento. Este comportamento é ilustrado na Figura 1.
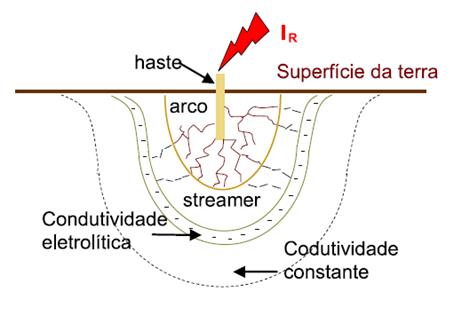
Figura 1 – Representação da ruptura dielétrica
do solo (ionização) ao redor de um eletrodo de aterramento.
Fonte: [17].
Nestas regiões de arco e streamers, a resistividade elétrica do
solo diminui de forma não linear até um valor muito baixo, se comportando como
um material bom condutor. Desta forma, o solo ionizado passa a atuar como uma
extensão do eletrodo, podendo ser considerado que houve um acréscimo no
diâmetro e no comprimento dele. Consequentemente, a resistência do aterramento
também irá sofrer uma variação não linear, reduzindo seu valor durante a parte
do transitório eletromagnético em que a ionização do solo se manifesta [17].
2.3
Modelo
Geométrico da ionização do solo
De
acordo com o Modelo Geométrico [1, 2, 5, 6], a
corrente no ponto de injeção do eletrodo de aterramento, necessária para
atingir o gradiente de potencial elétrico crítico que provoca a disrupção no
solo é determinada por,
|
|
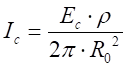
|
(3)
|
onde Ec
(kV/m), é o campo elétrico crítico, que pode ser estimado pela Equação (2), ρ
(Ω∙m) e R0 (Ω) são, respectivamente, a resistividade do
solo é a resistência do aterramento para baixas correntes, antes do processo de
ionização ocorrer. A resistência R0 depende da geometria do
aterramento, conforme descrito no item 2.1. Para correntes maiores que Ic,
a disrupção no solo continua a se espalhar, atingindo uma distância radial
limitada por,
|
|
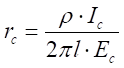
|
(4)
|
onde l (m) é o
comprimento longitudinal do eletrodo de aterramento. Nesta região ionizada do
solo a resistividade tende a zero, podendo ser considerada como um material
condutor perfeito, uma extensão do eletrodo. Uma representação esquemática do
fenômeno é apresentada na Figura 2.
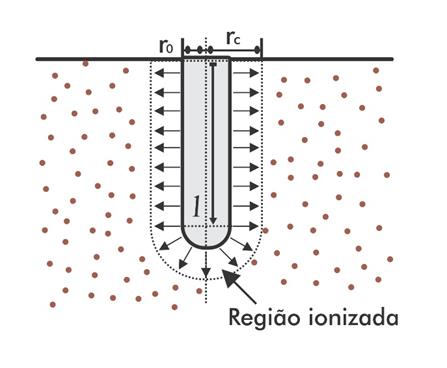
Figura 2 - Região ionizada do solo no entorno do
eletrodo de aterramento, conforme o Modelo Geométrico.
Fonte: Adaptada de [6].
Desta forma, a
resistência do aterramento deixa de ser constante e passa a ter um
comportamento dinamico não linear, representada por,
|
|
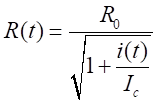
|
(5)
|
onde i(t) é a corrente
transitória do surto atmosférico que atinge o eletrodo de aterramento. Assim,
segundo o Modelo Geométrico, no processo da incidência da descarga atmosférica
no aterramento, a resistência inicial do eletrodo é mantida até que a corrente
de surto ultrapasse o valor crítico, quando a ionização no solo ao redor do
eletrodo é desencadeada. A partir daí, ocorre a diminuição da resistência,
representada por (5). Conforme o surto vai se dissipando e a corrente
diminuindo seu valor após atingir o pico, a resistência de aterramento retorna
gradualmente ao seu patamar inicial R0.
2.4
Modelo
Dinâmico da ionização do solo
A proposta do Modelo Dinâmico
parte da premissa de quantificar a variação não linear da resistividade
elétrica do solo ao longo do período transitório da descarga, considerando as
etapas de ionização e deionização.
Na
condição da ionização do solo não acontecer, a resistividade do solo permanece
constante, sendo denominada de resistividade inicial ρ0.
Entretanto, assim que a corrente escoada pelo aterramento aumentar de
intensidade, ao ponto do campo elétrico ultrapassar o valor limite para a
ocorrência da ruptura dielétrica do solo – dando início ao processo de
ionização – a resistividade passará a ter um forte comportamento não linear,
decrescendo em relação ao valor inicial ρ0 e posteriormente
retornando ao mesmo, na medida em que a intensidade da corrente do surto diminui
após ter atingido o pico [8, 9]. Este comportamento pode ser representado
como um ciclo histerético, conforme mostrado na Figura 3.
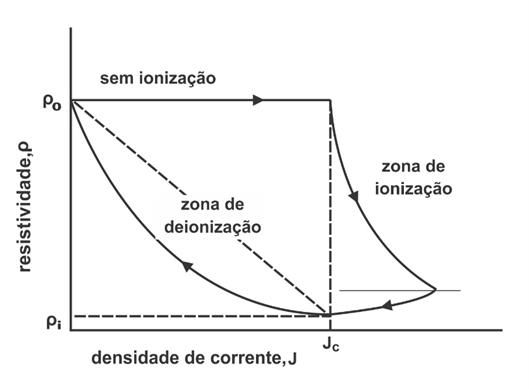
Figura 3 - Comportamento da resistividade do solo no aterramento durante
o processo de ionização, segundo o Modelo Dinâmico.
Fonte: Adaptada
de [8].
Desta forma, a
resistividade do solo é definida conforme as seguintes condições:
Para J < Jc
(etapa inicial):
|
|
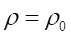
|
(6)
|
onde J (A/m2)
é a densidade superficial de corrente transitória na região do solo no entorno
do eletrodo de aterramento e Jc é o correspondente valor
crítico ou limite, a partir do qual inicia-se a ionização. A relação entre Jc
e o campo elétrico crítico Ec pode ser estabelecida a partir
da lei de Ohm localizada (ou relação constitutiva para condução elétrica em
materiais):
|
|
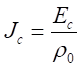
|
(7)
|
Para a obtenção de J,
considerando a distribuição da corrente uniforme na superfície equipotencial
que envolve o eletrodo de aterramento, tem-se:
|
|
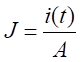
|
(8)
|
em que i(t) representa
a corrente transitória de surto proveniente da descarga atmosférica e A(m2)
é a área da superfície equipotencial do potencial elétrico no solo, obtida pela
somatória da parede lateral de um cilindro com comprimento l igual ao do
eletrodo e uma superfície hemisférica de raio r, correspondente à parte
inferior do eletrodo (ver Figura 2):
|
|
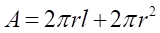
|
(9)
|
·
Para J ≥ Jc (etapa de ionização):
Nesta situação, inicia-se o
processo de ionização, onde a resistividade se torna variável e com valores
menores que o inicial (ρ<ρ0). A mesma é descrita como:
|
|
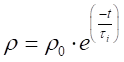
|
(10)
|
onde t é o instante de
tempo computado a partir do início da ionização e τi é a
constante de tempo de ionização.
·
Para J < Jc (etapa de deionização):
Após a corrente de surto
atingir seu valor máximo, a ionização continuará a acontecer até o campo
elétrico enfraquecer e ficar abaixo do ponto crítico (E < Ec).
Nesse instante, inicia-se o processo de deionização, no qual a resistividade do
solo tende a crescer, retornando ao seu valor original ρ0 no
final do transitório. Nesta etapa, o comportamento da resistividade é definido
como
|
|
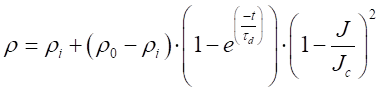
|
(11)
|
sendo ρi (Ω∙m)
a resistividade mínima, atingida no instante que marca o início da etapa de
deionização e τd é a constante de tempo de
deionização.
As constantes de tempo de
ionização (τi) e de deionização (τd) são
determinadas empiricamente, a partir de resultados experimentais [8, 10].
Nos próximos itens será apresentada
a aplicação dos Modelos Geométrico e Dinâmico no ATP, a partir do uso da
ferramenta Models.
3
Método
da pesquisa
3.1
Implementação
computacional no ATP
O ATP possui uma
extensa gama de recursos para a modelagem de sistemas de potência, sendo um dos
programas mais utilizados pelos pesquisadores da área para a simulação de redes
elétricas envolvendo transitórios eletromagnéticos. A principal ferramenta do
ATP aplicada neste trabalho foi a rotina de suporte Models, que permite
ao usuário configurar blocos contendo modelos de equipamentos e componentes que
apresentam comportamento não linear. Neste caso, foram implementadas em Models
as formulações matemáticas apresentadas no item 2, que consideram a ionização
do solo nos aterramentos pelo Modelo Dinâmico e pelo Modelo Geométrico.
Os casos de estudo corresponderam a RAD do tipo compactas,
com parâmetros reais utilizados pelas concessionárias de energia. A Figura 4
ilustra esquematicamente um trecho das redes estudadas, sendo atingido de forma
direta por uma descarga atmosférica, que incide no cabo de guarda.

Figura 4 - Trecho de RAD compacta (lado primário),
atingida por descarga atmosférica direta.
Fonte: Dos autores.
Neste artigo, será apresentada a modelagem e simulação para
um trecho de 350 metros de comprimento. Foi considerado apenas o lado primário
da linha (média tensão de 23,5 kV). O segmento de rede possui 5 postes, com
vãos entre eles de 70 metros. A Figura 6 apresenta um exemplo do circuito ATP
implementado para modelar este trecho de rede.
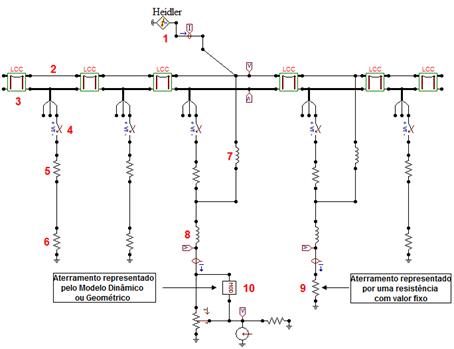
Figura 5 - Circuito ATP para a modelagem de um trecho
de RAD compacta (lado primário).
Fonte: Dos autores.
Os
elementos componentes que conformam o modelo ATP de RAD da Figura 5 são
descritos a seguir:
1. Surto
de corrente da descarga atmosférica (excitação do modelo). Representado por uma
curva do tipo dupla exponencial, conforme a Equação de Heidler [19],
|
|
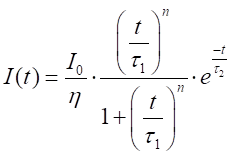
|
(12)
|
onde τ1 e τ2
são as constantes de tempo que determinam o tempo de subida e de cauda, n
o fator de inclinação da corrente e η um fator de correlação da corrente
de pico. O surto é injetado no cabo guarda, representado uma descarga direta.
2. Cabo
guarda ou mensageiro;
3. Elemento
“LCC” que representa os cabos das fases como linhas de transmissão (incluindo parâmetros
geométricos e materiais);
4. Chave
controlada por tensão que representa a ruptura dielétrica dos pinos isoladores,
quando o nível básico de isolamento destes é ultrapassado (no caso, 150 kV);
5. Resistência
dos postes (de concreto, tipo Duplo T), definida como [20],
|
|
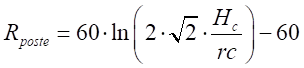
|
(13)
|
onde Hc é a
altura média dos postes e rc é o raio médio da base, ambos em metros.
6. Resistência
de aterramento para os casos dos postes não aterrados (representando o
engastamento do poste no solo). O valor é igual a duas vezes o da resistência
de aterramento constante aplicada nos postes aterrados [21];
7. Indutância
do cabo de ligação entre o cabo de cobertura e o cabo de descida, com valor de 1,2µH;
8. Indutância
do cabo descida, que faz a ligação com o eletrodo de aterramento, com valor de 11µH;
9. Resistência
de aterramento “convencional” (valor constante), quantificada pela Equação (1).
Representa o eletrodo de aterramento (hastes verticais);
10. Resistência
de aterramento transitória, considerando a ionização do solo (pelo Modelo
Dinâmico ou pelo Modelo Geométrico). O bloco Models comporta os
procedimentos matemáticos descritos no item 2.
3.2 Situações simuladas no ATP
As simulações foram executadas considerando que o poste
próximo ao ponto onde ocorre a descarga está aterrado e todos os outros estão
sem aterramento. Neste poste aterrado, foram avaliados os
seguintes casos para representar o eletrodo de aterramento:
·
Aterramento representado por uma resistência de valor constante, conforme
Equação (1) e o elemento 9 da Figura 5;
·
Aterramento representado por uma resistência transitória, considerando
a ionização pelo Modelo Dinâmico. Neste caso a ferramenta Models é
aplicada (elemento 10 da Figura 5);
·
Aterramento representado por uma resistência transitória, considerando
a ionização pelo Modelo Geométrico. Neste caso a ferramenta Models é
aplicada (elemento 10 da Figura 5).
As grandezas e parâmetros analisados após a execução das
simulações foram (ver Figura 6):
·
Sobretensão transitória no cabo de cobertura, no ponto de impacto
da descarga atmosférica;
·
Sobretensão transitória nas fases de média tensão (lado
primário), no ponto da descarga;
·
Tensão e corrente no eletrodo de aterramento pelo qual acontece o
escoamento da corrente de descarga atmosférica;
·
Resistência dinâmica no eletrodo de aterramento, nas situações em
que o modelo de aterramento considera a ionização do solo.
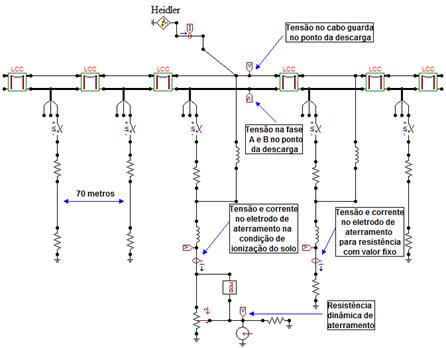
Figura 6 – Identificação das grandezas e parâmetros
obtidos a partir das simulações ATP da RAD compacta.
Fonte: Dos autores.
4
Resultados
da pesquisa
Nesta
seção serão apresentados os resultados das simulações ATP para a RAD compacta
descrita no item 3, quando atingida por uma descarga atmosférica direta.
Especificamente, para as simulações do presente trabalho foi considerado um
solo com resistividade elétrica aparente de 80 (Ω∙m). Assim, o campo elétrico
crítico, calculado pela Equação (2), é de 618 (kV/m). Como eletrodo de
aterramento foi aplicada uma haste vertical de 2,4 (m) de comprimento e seção
transversal de 0,0124 (m) de diâmetro, apresentando uma resistência de
aterramento de 33 (Ω), obtida a partir da Equação (1). No caso do surto
atmosférico, modelado por (12), foi considerada uma corrente de pico de 35
(kA), um tempo de subida de 5,6 (μs) e um tempo de cauda de 75 (μs). Na
situação em que o Modelo Dinâmico foi aplicado, as constantes de tempo de
ionização e deionização utilizadas foram τi =1,5 (μs) e τd
= 0,5 (μs) respectivamente, conforme Darveniza et al [8].
Na Figura 7 são apresentadas as curvas de sobretensão
transitória no cabo guarda, para os três modelos de aterramento avaliados.
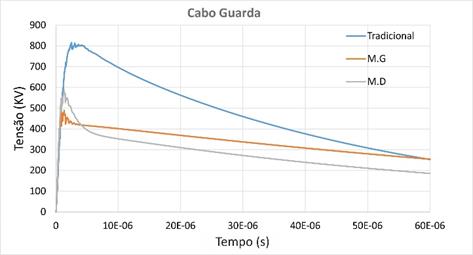
Figura 7 - Sobretensões no cabo guarda. Aterramento
representado por uma resistência fixa (azul), aterramento representado
pelo Modelo Geométrico (laranja) e aterramento representado pelo Modelo Dinâmico
(cinza).
Fonte: Dos autores.
Percebe-se na Figura 7 que a sobretensão no caso em que se
considera o aterramento como uma resistência fixa é nitidamente maior quando
comparada às situações em que a ionização do solo é incluída. Por outro lado,
no comparativo entre os resultados para as configurações onde o aterramento
sofre a ionização, o Modelo Dinâmico atingiu um pico maior de sobretensão, mas
a queda é ligeiramente mais acentuada do que para o Modelo Geométrico,
registrando valores menores no final do transitório. Esta tendência de
comportamento apresentada pelas sobretensões no cabo de guarda se repete nas
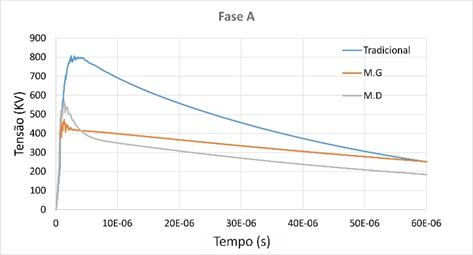
fases do primário da rede, conforme pode ser observado na Figura 8.
O
comportamento da curva de sobretensão na fase C não foi mostrado na Figura 8
pelo fato de ser idêntico ao da fase A, devido à simetria transversal da
disposição dos cabos na configuração da rede compacta. Para todas as situações,
as fases A e C tiveram valores de pico de sobretensão ligeiramente inferiores
aos do cabo guarda, mas sempre superiores aos níveis atingidos pela fase B,
pelo fato desta última estar mais afastada.
(a)
(b)
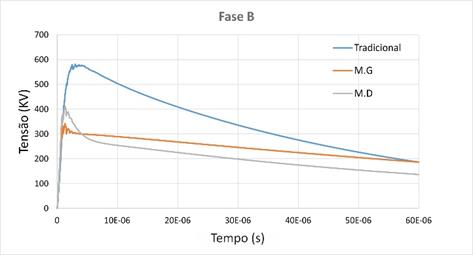
Figura 8 - Sobretensões nas fases. Aterramento
representado por uma resistência fixa (azul), aterramento representado pelo
Modelo Geométrico (laranja) e aterramento representado pelo Modelo Dinâmico
(cinza). a) Fase A; b) Fase B.
Fonte: Dos autores.
Na
figura 9 são mostrados os resultados para os níveis de sobretensão no ponto de
injeção do eletrodo de aterramento.
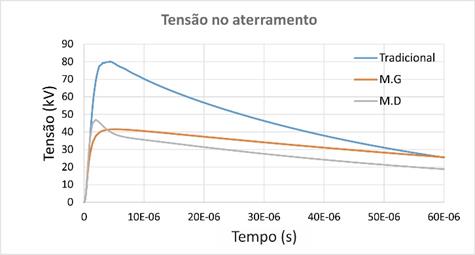
Figura 9 – Níveis de sobretensão no eletrodo de aterramento. Aterramento
representado por uma resistência fixa (azul), aterramento representado pelo
Modelo Geométrico (laranja) e aterramento representado pelo Modelo Dinâmico
(cinza).
Fonte: Dos autores.
Novamente,
nota-se que quando a ionização do solo é considerada no aterramento, os valores
de tensão são menores em relação ao caso com valor fixo de resistência.
Os
níveis de corrente no ponto de injeção do eletrodo de aterramento são
apresentados na Figura 10.
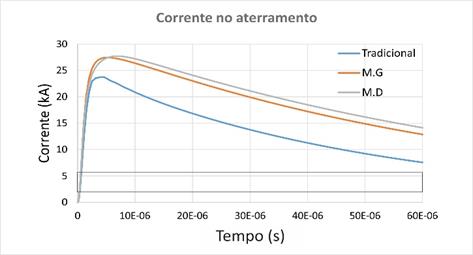
Figura 10 - Níveis de corrente no eletrodo de
aterramento. Aterramento representado por uma resistência fixa (azul),
aterramento representado pelo Modelo Geométrico (laranja) e aterramento
representado pelo Modelo Dinâmico (cinza).
Fonte: Dos autores.
No
caso das correntes, a amplitude é maior quando se considera a ionização do
solo, já que nessa situação a resistência de aterramento possui um
comportamento dinâmico não linear, com uma forte queda nos momentos iniciais do
transitório. Desta forma, a corrente da descarga ecoa com maior facilidade
através do aterramento, de forma mais acentuada do que para as mesmas condições
da RAD, mas com o uso do modelo convencional de resistência de aterramento
constante.
A
Figura 11 apresenta o comportamento transitório da resistência de aterramento
durante a descarga
atmosférica, segundo os modelos matemáticos
que consideram o fenômeno da ionização do solo.
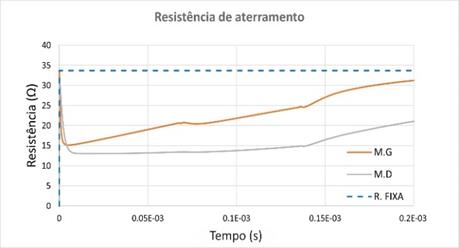
Figura 11 – Resistência de aterramento na condição
de ionização do solo. Aterramento representado pelo Modelo Geométrico (laranja)
e aterramento representado pelo Modelo Dinâmico (cinza).
Fonte: Dos autores.
A
partir dos resultados da Figura 11 é possível comprovar que o comportamento
entre os dois modelos de resistência aterramento é muito similar. Ambos partem
de um valor muito próximo da resistência constante (sem ionização do solo),
sendo que a curva do Modelo Geométrico sofre menos diminuição do seu valor e
deioniza mais rapidamente que para o caso do Modelo Dinâmico.
As
Tabelas 1 e 2 sintetizam os principais resultados obtidos.
Tabela
1 - Comparativo dos resultados mais
significativos obtidos nas simulações ATP da RAD (valores máximos).
|
Grandeza
|
Condição do Modelo de Aterramento
|
|
|
Resistência Fixa
|
Modelo Dinâmico
|
Modelo Geométrico
|
|
|
|
Tensão no Cabo Guarda (kV)
|
825
|
633
|
553
|
|
|
Tensão na Fase A (kV)
|
815
|
612
|
532
|
|
|
Tensão na Fase B (kV)
|
585
|
442
|
386
|
|
|
Tensão no Aterramento (kV)
|
81,4
|
49,3
|
46,3
|
|
|
Corrente no Aterramento (kA)
|
23,49
|
27,89
|
27,55
|
|
Fonte:
Dos autores.
Tabela 2 – Desvio relativo entre os resultados para
os três modelos de resistência de aterramento.
|
Grandeza
|
Desvio Relativo (%) entre:
|
|
|
Modelo Dinâmico
e Resistência Fixa
|
Modelo Geométrico e Resistência Fixa
|
Modelo Dinâmico
e
Modelo Geométrico
|
|
|
|
Tensão no Cabo Guarda
|
23,3
|
33,0
|
12,6
|
|
|
Tensão na Fase A
|
24,9
|
34,7
|
13,1
|
|
|
Tensão na Fase B
|
24,4
|
34,0
|
12,7
|
|
|
Tensão no Aterramento
|
39,4
|
43,1
|
6,1
|
|
|
Corrente no Aterramento
|
-11,2
|
-10,0
|
1,0
|
|
Fonte:
Dos autores.
Verifica-se
que para todas as simulações realizadas os valores de pico de tensão sempre são
menores nas situações em que a ionização do solo foi considerada. Também se
observou que no comparativo entre os Modelos Dinâmico e Geométrico, o primeiro
apresentou valores de pico maiores, tanto para as tensões (nos cabos e
aterramento), quanto para a corrente no ponto de injeção do aterramento.
Em
relação aos tempos de processamento computacional, as simulações envolvendo o
modelo Geométrico levaram apenas cinco (05) segundos, enquanto aquelas
utilizando o modelo Dinâmico demandaram em torno de noventa (90) segundos. Os
recursos empregados nas simulações foram um Notebook com Processador Intel®
Core™ i5-4210U CPU @ 1.70GHz 2.40 GHz, Memória RAM de 4,00 GB e Sistema
Operacional Windows 10 de 64 Bits.
5
Conclusões
O
desenvolvimento deste trabalho veio a contribuir para a análise mais realista
dos processos transitórios que acontecem nas redes aéreas de distribuição de
energia, decorrentes de descargas atmosféricas. O principal objetivo foi
desenvolver um estudo comparativo de modelos do aterramento elétrico, com e sem
a consideração do fenômeno da ionização do solo, visando avaliar seus efeitos
nos níveis das tensões e correntes, tanto nas fases do lado primário da rede,
quanto na própria topologia de aterramento.
A
incorporação do equacionamento dos modelos Dinâmico e Geométrico da ionização
do solo no ATP, utilizando a ferramenta Models, viabilizou a interação
entre o subsistema de aterramento (com comportamento transitório) e as demais
estruturas componentes da rede de distribuição de energia.
Em
relação ao comparativo direto entre os dois modelos de aterramento elétrico com
ionização do solo (Dinâmico e Geométrico), pode ser ponderado que as diferenças
entre os resultados obtidos não foram muito significativas. Desta forma,
avalia-se que o Modelo Geométrico seja mais indicado para efetuar simulações de
redes aéreas de distribuição. Pesou nesta decisão a formulação mais simples,
sua facilidade de implementação computacional, o menor tempo de processamento
das simulações e o fato de depender apenas de um parâmetro experimental, que é
a resistividade elétrica aparente do solo. Por outro lado, o Modelo Dinâmico
traz uma representação mais física do comportamento do solo, ao quantificar
diretamente as variações da resistividade durante todo o processo transitório.
No entanto, apresenta uma importante limitação, que é a dependência do seu
equacionamento de dois coeficientes experimentais (constantes de tempo de
ionização e deionização), de difícil obtenção e sobre os quais existem poucas
informações na literatura.
De
qualquer forma, os resultados da pesquisa enfatizaram a importância da
consideração do fenômeno da ionização do solo nos estudos das redes aéreas de
distribuição. Para uma condição típica de descarga atmosférica direta, a
probabilidade da ruptura dielétrica do solo é elevada, levando à redução severa
da resistividade elétrica do solo no entorno do eletrodo e, consequentemente,
da resistência de aterramento.
De
fato, as situações simuladas constataram que, para todos os casos, os níveis de
sobretensões tanto no cabo de guarda quanto nas fases da linha foram muito
superiores quando a ionização do solo não é considerada no modelo do
aterramento.
No
caso das correntes injetadas no eletrodo de aterramento, as magnitudes foram
maiores para os casos em que a ionização do solo foi contemplada. Isto
significa que uma parcela considerável da descarga é dissipada através do
próprio sistema de aterramento, propiciando que menores níveis de corrente se
propaguem através das fases da rede durante o processo da descarga atmosférica.
Desta forma, a partir deste estudo foi percebido que a incorporação do
fator “ionização do solo no aterramento” nas etapas de projeto de redes aéreas
de distribuição poderia levar a uma análise menos conservadora para a escolha
de algumas das estruturas componentes destas redes (ex. dispositivos de
proteção e isoladores), contribuindo na redução de custos.
Referências
[1] IEEE 1410: IEEE Guide for improving
the lightning performance of electric power overhead distribution lines. IEEE
Power Engineering Society, 2004.
[2] COORAY, V. Lightning
protection. Stevenage: Institution of Engineering and Technology, 2010.
[3] GRCEV, L. Modeling of
grounding electrodes under lightning currents. IEEE Transactions on
Electromagnetic Compatibility, v. 51, p. 559-571, 2009.
[4] KORSUNTCEV, A. V.
Application of the theory of similitude to the calculation of concentrated
earth electrodes. Electrichestvo, p. 31-35, 1958.
[5] CIGRE Task
Force on Soil Ionization – WG 33.01. Perspectives on soil ionization
investigation, p. 105-106, 2000.
[6] SEKIOKA, S. Discussion of
CIGRE current-dependent grounding resistance model. 2013 International
Symposium on Lightning Protection, SIPDA 2013, p. 184-189, 2013.
[7] MATA, C. T. et
al. EMTP
modeling of a triggered-lightning strike to the phase conductor of an overhead
distribution line. IEEE Transactions on Power Delivery, v. 15, p. 1175-1181,
2000.
[8] LIEW, A. C.;
DARVENIZA, M. Dynamic
model of impulse characteristics of concentrated earths. Proceedings of the
Institution of Electrical Engineers, v. 121, p. 123-135, 1974.
[9] WANG, J.; LIEW,
A. C.; DARVENIZA, M. Extension of dynamic model of impulse behavior of concentrated grounds at
high currents. IEEE Transactions on Power Delivery, v. 20, p. 2160-2165, 2005.
[10] ALA, G. et al.
Finite difference time domain simulation of earth electrodes soil
ionization under lightning surge condition. IET Science, Measurement and
Technology, p. 134-145, 2008.
[11] SANTOS,
T. L. T.; OLIVEIRA, R. M.S.; SOBRINHO, C. L and ALMEIDA, J. F. Soil Ionization
in Different Types of Grounding Grids Simulated by FDTD Method. The SBMO/IEEE
MTT-S International Conference on Microwave and Optoelectronics Conference,
2009, Belém - Brazil.
[12] MATA, C.
T.; FERNANDEZ,
M. I.; RAKOV, V. A. and UMAN M. A. EMTP Modeling of a Triggered-Lightning
Strike to the Phase Conductor of an Overhead Distribution Line. IEEE Transactions
on Power Delivery, v. 15, n. 4, p. 1175-1181, 2000.
[13] GONDIM, I.N.; OLIVEIRA, J.;
TAVARES, C.E.; BARBOSA, J.A.F. and MENDOÇA, M.V.B. Grounding system modelling
and its impact on computational refunding analysis for equipment damages.
Renewable Energy and Power Quality Journal, p. 917-922, 2011.
[14] SUNDE, E. D. Earth
conduction effects in transmission systems, New York: Dover
Publications, 1968.
[15] KINDERMANN, G.; CAMPAGNOLO, J. M. Aterramento
Elétrico. Porto Alegre: Ed. Sagra – DC Luzzatto, 1995.
[16] SALDANHA, J. O. P. et al. Proteção de
equipamentos elétricos e eletrônicos contra surtos elétricos em instalações,
Lagoa Santa: Editora Clamper, 2016.
[17] TELLO, M. et al. Aterramento
elétrico impulsivo, em baixa e alta frequência, Porto Alegre: Ed. EdiPUCRS, 2007.
[18] OETTLE, E. A new general estimation
curve for predicting the impulse impedance of concentrated earth electrodes. IEEE
Transactions on Power Delivery, v. 3, p. 2020-2029, 1988.
[19] GAMEROTA, W. R. et al.
Current waveforms for lightning simulation. IEEE Transactions on
Electromagnetic Compatibility, v. 54, p. 880-888, 2012.
[20] CABRAL, R. J. et
al. Analysis of distribution lines performance against lightning using
ATP-EMTP. IEEE International Symposium on Electromagnetic Compatibility, p.
8-12, 2012, Rome- Italy.
[21] SEKIOKA, S.;
YAMAMOTO, K. and YOKOYAMA, S. Measurements of a concrete pole impedance with an impulse
current source. Proc. of International Conference on Power Systems Transients,
p. 457-462, 1995, Lisbon- Portugal.
orcid.org/0000-0002-3215-750X
orcid.org/0000-0001-5517-3900
orcid.org/0000-0001-9499-2757
orcid.org/0000-0001-8957-3902