¹Instituto Federal de Educação, Ciência e Tecnologia de Santa Catarina, Campus Florianópolis – Centro.

DOI: 10.25286/repa.v9i1.2232

Esta obra apresenta Licença Creative Commons Atribuição-Não Comercial 4.0 Internacional.

Como citar este artigo pela NBR 6023/2018: Juliano Bitencourt Padilha; Lisandra Kittel Ries. Estimativa das perdas ferromagnéticas em transformadores Revista de Engenharia e Pesquisa Aplicada, v.9, n. 1, p. 23-27, 2024. DOI: 10.25286/repa.v8i3.2232

RESUMO

As perdas energéticas em dispositivos eletromagnéticos apresentam duas principais parcelas: perdas no cobre, em condutores elétricos como cobre e alumínio, e ferromagnéticas, em núcleos de aço-silício. Ainda, as ferromagnéticas se dividem em três parcelas: por histerese, por correntes de Foucault e anômalas. De maneira geral, as perdas anômalas são menos significativas, podendo ser desprezadas. Este trabalho apresenta uma metodologia para estimar as perdas ferromagnéticas em transformadores a partir das características físicas e dimensões do núcleo. Abordando um exemplo, são apresentadas as etapas de cálculo a serem seguidas. Resultados obtidos experimentalmente para as perdas ferromagnéticas de dois transformadores reais também são apresentados.

PALAVRAS-CHAVE: transformadores, perdas ferromagnéticas, histerese magnética, correntes de Foucault.

ABSTRACT

Energy losses in electromagnetic devices have two main parts: copper losses, in electrical conductors, such as copper and aluminum, and ferromagnetic losses, in silicon steel cores. Also, the ferromagnetic ones are divided into three parts: by hysteresis, by eddy currents and anomalous. In general, anomalous losses are less significant and can be neglected. This work presents a methodology to estimate ferromagnetic losses in transformers from the physical characteristics and dimensions of the core. An example approach of the calculation steps to be followed are presented. Experimentally obtained results for the ferromagnetic losses of two real transformers are also presented.

KEYWORDS: transformers, ferromagnetic losses, magnetic hysteresis, eddy currents.

1 INTRODUÇÃO

Transformadores de tensão são máquinas elétricas utilizadas com a função de abaixar ou elevar tensões em um sistema elétrico. São constituídos basicamente de enrolamentos (primário e secundário) e por um núcleo ferromagnético. Os enrolamentos são formados por alumínio ou cobre e o núcleo ferromagnético por lâminas de aços para fins elétricos. Em termos de perda energética, diferença entre a energia entregue ao primário e a energia entregue à carga conectada ao secundário, temos que as principais perdas estão associadas às resistências elétricas dos enrolamentos (perdas no cobre) e às perdas ferromagnéticas (histerese magnética e correntes de Foucault, desprezando as perdas anômalas). Normalmente as perdas ferromagnéticas são consideradas constantes, independentemente do nível de carregamento da máquina [1].

Uma vez que a corrente de magnetização é reduzida em transformadores, na operação a vazio o consumo energético da máquina é quase que em sua totalidade devido às perdas ferromagnéticas (as perdas no cobre podem ser desprezadas nessa situação). Assim, com o ensaio a vazio da máquina, podemos determinar as perdas ferromagnéticas. Já as perdas no cobre dependem do nível de carregamento da máquina.

Em muitos casos, os transformadores operam 24 horas por dia, como por exemplo, os de distribuição. Uma vez que em boa parte do dia o carregamento da máquina é reduzido, é interessante que as perdas ferromagnéticas não sejam elevadas. Assim, é natural que as concessionárias de energia exijam baixos valores para as perdas ferromagnéticas em comparação com as perdas totais. Por exemplo, a concessionária Centrais Elétricas de Santa Catarina (CELESC) exige para transformadores trifásicos de 75 kVA, tensão máxima de 15 kV, uma perda a vazio máxima da ordem de 270 W e perda total máxima de 1345 W [2].

Neste contexto, observa-se o quão importante é a quantificação das perdas ferromagnéticas. Ainda, cabe destacar que o estudo dessas perdas abrange uma vasta área de pesquisa e muitos trabalhos referentes ao assunto podem ser encontrados na literatura [3][4].

Em suma, este trabalho apresenta, ao abordar um exemplo, uma metodologia para estimar as perdas ferromagnéticas em transformadores a partir das características físicas e dimensões do núcleo. Cada etapa ao longo da metodologia é descrita detalhadamente com as respectivas equações utilizadas apresentadas. Posteriormente, resultados obtidos experimentalmente para dois transformadores reais também são apresentados e uma comparação com a estimativa inicial é realizada.

2. Fundamentos sobre perdas ferromagnéticas

Nesta seção é apresentado um breve compilado teórico sobre perdas ferromagnéticas. Informações mais detalhadas sobre o assunto podem ser obtidas por meio das referências citadas ao longo deste artigo.

Na sequência, as três componentes dessas perdas são descritas e, por fim, é apresentada a forma mais comumente utilizada para o ensaio de materiais ferromagnéticos.

2.1. Histerese magnética

Assumindo que um material esteja submetido a um campo magnético periódico senoidal de determinada frequência, o material percorrerá o ciclo de histerese, um ciclo que relaciona o campo magnético com a indução magnética. De forma simplificada, percorrer este ciclo significa fazer com que os domínios de Weiss troquem suas polaridades magnéticas, o que exige o dispêndio de certa quantidade de energia [5][6][7]. Uma representação desses domínios pode ser observada na Figura 1.

Figura 1 – Representação dos domínios de Weiss.

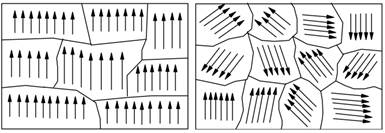
Fonte: SOUZA e JARDIM [8].

Para induções entre 0,2 e 1,8 T é possível fazer uso da equação Steinmetz para determinação das perdas por histerese. Essa equação é dada por [5][6]:

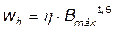(1)

Onde: w_h é a perda por histerese (em J/m³), η é uma constante que depende do material e B_máx é indução máxima (em T).

Para determinar as perdas em W, P_h, basta multiplicar o resultado obtido em (1) pela frequência f (em Hz) e pelo volume v de material (em m³):

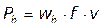(2)

2.2. Correntes de Foucault

Uma vez que os materiais ferromagnéticos apresentam certa condutividade elétrica, e estando os mesmos submetidos a campos variáveis no tempo, é esperado o surgimento de correntes parasitas no material. Tais correntes produzem aquecimento e o que chamamos de perdas por correntes de Foucault.

Assumindo uma lâmina de material ferromagnético, conforme Figura 2, que está submetida a uma indução senoidal em uma única direção, as perdas por correntes de Foucault podem ser deduzidas como [5][6]:

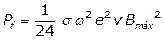(3)

Onde: P_f é a perda por correntes de Foucault (em W), σ é a condutividade do material (em S/m), ω é a frequência angular (em rad/s, é igual a 2ϖf), e é a espessura da lâmina (em m).

Figura 2 – Lâmina de material ferromagnético submetida a uma indução variável na direção x.

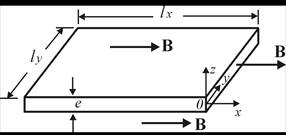
Fonte: BASTOS [5].

2.3. Perdas anômalas ou excedentes

Essas perdas representam, em geral, uma parcela relativamente pequena das perdas ferromagnéticas totais [5].

A modelagem matemática dessas perdas pode ser expressa por [9]:

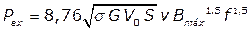(4)

Onde: P_ex é a perda excedente (W), G é uma constante adimensional, V₀ é um parâmetro associado ao material (em A/m) e S é a área da seção transversal do material (em m²).

2.4. Quadro de Epstein

Para o ensaio de materiais ferromagnéticos, o método mais comumente utilizado faz uso do quadro de Epstein [10].

O quadro Epstein (Figura 3) é composto por um enrolamento primário e um secundário, de modo que, durante o ensaio, o quadro se comporta como um transformador operando a vazio.

Figura 3 – Quadro de Epstein comercial.

Fonte: BROCKHAUS (Epstein Frame) [11].

A amostra de material a ser ensaiada deve ser preparada como um conjunto de várias lâminas que deve sempre ser um múltiplo de quatro, pois o quadro apresenta quatro ramos.

Caso o ensaio seja realizado em baixa frequência, por exemplo, em 1 Hz, podemos assumir que o laço de histerese obtido do ensaio compreende apenas as perdas por histerese. Já para frequências superiores, como por exemplo, 60 Hz, o laço compreende as perdas ferromagnéticas totais (histerese, correntes de Foucault e anômalas). Exemplos de laços para diferentes frequências podem ser observados na Figura 4. Esses foram obtidos a partir do modelo apresentado em [12].

Figura 4 – Laços de histerese dinâmicos.

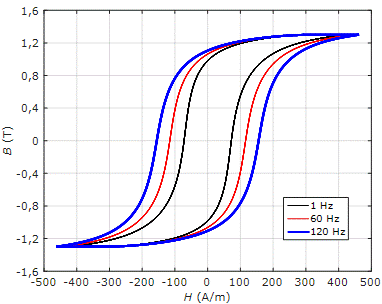
lacos.emf

Fonte: Elaboração própria.

3. Método e resultados obtidos

Considere-se um transformador monofásico do tipo núcleo envolvente, conforme o apresentado na Figura 5. Esse tipo de núcleo apresenta três colunas verticais, onde a coluna central tem o dobro da largura das laterais e nela os enrolamentos (primário e secundário) ficam localizados de forma concêntrica.

Figura 5 – Núcleo envolvente a ser analisado.

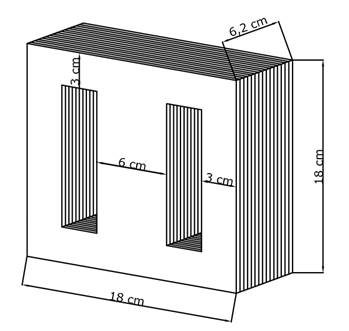
Fonte: Elaboração própria.

Assume-se que o material ferromagnético apresenta lâminas de 0,5 mm e é do tipo Aperam E230 (referência comercial) [13]. As características desse material estão presentes na Tabela 1. Adotou-se esse tipo, pois os transformadores ensaiados (resultados apresentados no item 3.5) são de baixo custo e possivelmente apresentam chapas de menor qualidade (observa-se que a referência E230 é a que apresenta maiores perdas na Tabela 1). Ainda, o catálogo completo do fabricante também informa as características para outras espessuras de lâminas.

Tabela 1 – Características de alguns aços para fins elétricos comerciais.

Características Garantidas
Produto		Espessura (mm)	Perda Magnética Máxima a (W/kg)				Indução Magnética Mínima a (W/kg)			Densidade Assumida (g/cm³)	Fator de Empilhamento Mínimo (%)	Índice de Dobramento Mínimo
Referência	Aperam		1,0 T		1,5 T		2500 A/m	5000 A/m	10000 A/m
Referência	Aperam		50 Hz	60 Hz	50 Hz	60 Hz	2500 A/m	5000 A/m	10000 A/m
P400-50A (1)	E233	0,50	1,70	2,15	3,68	4,66	1,64	1,73	1,83	7,75	97,0	10
M530-50A	E230		2,30	2,91	5,30	6,66	1,59	1,69	1,79
M470-50A	E185		1,85	2,34	4,10	5,19
M400-50A	E170		1,70	2,15	3,68	4,66						5
M370-50A	E157		1,57	2,00	3,42	4,33
M350-50A	E145		1,45	1,84	3,33	4,22
M330-50A	E137		1,37	1,74	3,14	3,98	1,58	1,67	1,78	7,65		3
M310-50A	E125		1,25	1,58	3,05	3,85
M290-50A	E115		1,15	1,45	2,90	3,65
M270-50A	E110		1,10	1,40	2,70	3,45
M250-50A	E105		1,05	1,35	2,50	3,20
M230-50A	E100		1,00	1,30	2,30	2,95

Fonte: APERAM (Aços Elétricos de Grão Orientado e de Grão Não-Orientado) [13].

Outros dados a serem considerados são a tensão de alimentação do primário (assume-se 220 V – 60 Hz) e o número de espiras do primário (assume-se 220 espiras).

3.1. Cálculo do fluxo magnético máximo na coluna central

Inicialmente, considerando que todo o fluxo é enlaçado pela bobina primária, é calculado o fluxo magnético máximo na coluna central do transformador a partir da seguinte equação [1]:

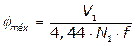(5)

Onde: Φ_máx é o fluxo magnético máximo (em Wb), V₁ é a tensão eficaz de alimentação do primário (em V), N₁ é o número de espiras do primário e f é a frequência da tensão de alimentação (em Hz).

Para o exemplo analisado, tem-se que Φ_máx = 3,754 mWb. Cabe destacar que nas colunas laterais, desconsiderando efeitos de fluxos dispersos, o fluxo é a metade do obtido na coluna central.

3.2. Cálculo da indução magnética máxima

A indução magnética máxima é igual tanto na coluna central como nas colunas laterais, ainda, assume-se o valor da mesma igual ao longo de todo o núcleo. A indução pode ser obtida da divisão entre o fluxo magnético pela área que o mesmo atravessa, dessa forma tem-se que:

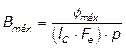(6)

Onde: l_C é a largura da coluna (em m), F_e é o fator de empilhamento (em termos unitários) e p é a profundidade do núcleo (em m).

Para o exemplo analisado, B_máx = 1,04 T.

3.3. Cálculo das perdas ferromagnéticas em W/kg

Desprezando as perdas anômalas, as perdas ferromagnéticas são compostas por duas parcelas, uma proporcional à B_máx^1,6 (perdas por histerese) e outra proporcional à B_máx^2,0 (perdas por correntes de Foucault), logo, inicialmente assume-se que:

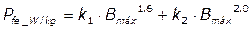(7)

Onde: P_{fe_W/kg} é a perda ferromagnética (em W/kg) e, k₁ e k₂ são constantes.

A indução presente na Tabela 1 é a máxima e na tabela são apresentados valores de P_{fe_W/kg} para dois valores de B_máx em 60 Hz. Dessa forma, é possível determinar os valores para k₁ e k₂ que satisfaçam o seguinte sistema:

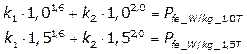(8)

Para o exemplo analisado, obtém-se k₁ = -0,3339 e k₂ = 2,5761, de forma que não é factível assumir essa abordagem, uma vez que k₁ resulta em um valor negativo. Isso ocorre pois observa-se que (P_{fe_W/kg_1,5T}/ P_{fe_W/kg_1,0T}) = 2,29, que é um valor maior que (1,5/1,0)² = 2,25, caracterizando que o aumento das perdas, segundo o fabricante das chapas, é diretamente proporcional a B_máx elevado a um expoente maior que 2, o que não está em concordância com a teoria abordada, referenciada e apresentada neste artigo. Assim, se fez necessária uma segunda modelagem matemática, tal que:

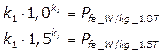(9)

A solução para o sistema apresentado em (9) é k₁ = 2,91 e k₂ = 2,042, logo, assumindo B_máx = 1,04 T, tem-se que P_{fe_W/kg} = 3,153 W/kg.

Cabe salientar que a separação e modelagem das perdas ferromagnéticas é um vasto campo de estudo, portanto, as considerações aqui apresentadas apenas visam a determinar o valor de P_{fe_W/kg} de uma forma mais criteriosa do que uma simples interpolação linear.

3.4. Cálculo das perdas ferromagnéticas totais em W

Considerando as dimensões apresentadas na Figura 5 e um fator de empilhamento de 97% (igual ao apresentado na Tabela 1), obtém-se um volume de material ferromagnético da ordem de 1515,528 cm³. Esse valor multiplicado pela densidade volumétrica do material (ver Tabela 1) resulta em uma massa de 11,745 kg. Por fim, multiplicando a massa pelo valor de P_{fe_W/kg} obtido anteriormente, obtém-se P_fe = 37,03 W, que é a perda ferromagnética total estimada para o núcleo analisado.

3.5. Resultados experimentais

Com as etapas descritas anteriormente, foi possível estimar as perdas ferromagnéticas do transformador. Para uma avaliação do que foi apresentado, determinou-se experimentalmente as perdas ferromagnéticas de dois transformadores com as mesmas dimensões e especificações do exemplo abordado. Tais transformadores são, a princípio, idênticos, pois são do mesmo modelo, de um mesmo lote, de um mesmo fabricante. As únicas variáveis desconhecidas para os transformadores ensaiados são o modelo das chapas (elas são de 0,5 mm, mas é desconhecida a referência) e o fator de empilhamento. Na Figura 6 temos a representação de um desses transformadores.

Figura 6 – Transformador monofásico ensaiado. Especificações: 1 kVA, 60 Hz, 220 V/(100-110-120) V, classe B, IP 00.

WhatsApp Image 2022-08-17 at 20.29.51.jpeg

Fonte: Elaboração própria.

Para a realização dos ensaios, considerou-se os transformadores operando a vazio com o lado de baixa tensão alimentado a partir de um alternador trifásico. Dessa forma, a partir do controle da velocidade do alternador, foi possível uma alimentação com as mais diversas frequências. O papel de máquina primária foi desempenhado por um motor de corrente contínua com excitação independente. Na Figura 7 tem-se a representação da bancada de ensaios.

Figura 7 – Bancada utilizada para os ensaios.

WhatsApp Image 2022-08-17 at 20.29.51 (1).jpeg

Fonte: Elaboração própria.

Os resultados obtidos experimentalmente estão presentes na Tabela 2.

Tabela 2 – Resultados experimentais. Para diferentes frequências, a relação V₁/f deve ser mantida constante e igual a 110/60 (de modo a resultar em um mesmo fluxo magnético). T1 e T2 fazem referência aos dois transformadores ensaiados e P_{fe_méd} é a média dos valores obtidos.

V₁ (V)	f (Hz)	P_{fe_}_T1 (W)	P_{fe_}_T2 (W)	P_{fe_méd} (W)
91,7	50	26,2	25,5	25,85
100,8	55	29,7	28,8	29,25
110,0	60	33,0	32,1	32,55
119,2	65	38,4	36,2	37,30
128,3	70	42,1	39,7	40,90
137,5	75	46,2	44,2	45,20
146,7	80	50,5	47,9	49,20
155,8	85	54,6	51,7	53,15
165,0	90	57,4	55,6	56,50

Fonte: Elaboração própria.

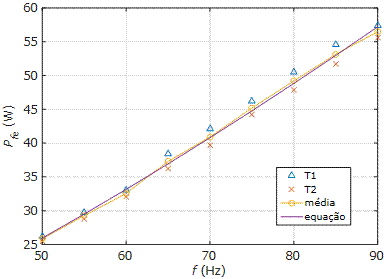
Pela Tabela 2 observa-se um aumento das perdas com o aumento da frequência, um resultado teoricamente esperado (ver equações (2), (3) e (4)). Essa relação entre frequência e perda é melhor observada com a Figura 8. A equação modelada, também ilustrada na Figura 4, é dada por:

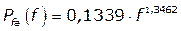(9)

Figura 8 – Perda ferromagnética em função da frequência.

grafico_final.emf

Fonte: Elaboração própria.

Embora uma análise quantitativa da diferença entre a estimativa inicial e o resultado experimental não seja precisa, uma vez que é desconhecida a especificação das chapas que compõem o núcleo, a Tabela 3 apresenta esse comparativo para as frequências de 50 e 60 Hz. Para as diferenças apresentadas na tabela, assumiu-se o resultado experimental como referência.

Tabela 3 – Comparativo entre resultados experimentais.

f (Hz)

experimental

P_{fe_méd} (W)

estimativa

P_fe (W)

diferença (%)

32,55

37,03

+13,76

25,85

29,29

+13,31

Fonte: Elaboração própria.

4. Conclusões

Neste trabalho uma metodologia que visa a estimar as perdas ferromagnéticas de um transformador foi apresentada. O exemplo abordado é de um transformador monofásico com núcleo envolvente, mas pode ser aplicada a transformadores com núcleo envolvido tanto monofásico quanto trifásico. Inicialmente um equacionamento matemático considerando dois termos para estimar as perdas ferromagnéticas foi assumido, um representando as perdas por histerese e o outro as perdas por correntes de Foucault. Dessa abordagem, um resultado inviável foi obtido para a constante referente às perdas por histerese, logo, uma nova abordagem se fez necessária. O novo equacionamento matemático parte do pressuposto de que, segundo os dados apresentados na Tabela 1 para o material E230, as perdas são proporcionais à B_máx elevado a um expoente maior que 2. Cabe destacar que o novo equacionamento é de simples compreensão e pode ser apresentado em cursos dos mais diversos níveis. Resultados experimentais para as perdas de dois transformadores também são apresentados para diferentes frequências de alimentação. Por fim, um comparativo entre as perdas estimadas e as experimentais foi realizado, indicando a coerência da metodologia utilizada.

Referências

[1] CHAPMAN, Stephen J. Fundamentos de Máquinas Elétricas. 5. ed. Porto Alegre: AMGH, 2013. 700 p. ISBN 978-8580552065.

[2] CELESC DISTRIBUIÇÃO S. A. E-313.0069 Transformador Pedestal para Redes de Distribuição Subterrâneas, [S. l.], 27 dez. 2021. Disponível em: https://www.celesc.com.br/arquivos/normas-tecnicas/especificacao-tecnica/E3130069.pdf. Acesso em: 17 ago. 2022.

[3] BATISTELA, Nelson Jhoe. Caracterização e Modelagem Eletromagnética de Lâminas de Aço ao Silício. Orientador: Nelson Sadowski. 2001. 227 p. Tese (Doutorado em Engenharia Elétrica) - Universidade Federal de Santa Catarina, Florianópolis/SC, 2001. Disponível em: https://repositorio.ufsc.br/xmlui/handle/123456789/81963. Acesso em: 17 ago. 2022.

[4] SIMÃO, Claudenei. Estudo da eficiência energética de dispositivos eletromagnéticos e de suas alimentações. Orientador: Nelson Sadowski. 2008. 134 p. Tese (Doutorado em Engenharia Elétrica) - Universidade Federal de Santa Catarina, Florianópolis/SC, 2008. Disponível em: https://repositorio.ufsc.br/handle/123456789/91281. Acesso em: 17 ago. 2022.

[5] BASTOS, João P. A. Eletromagnetismo para Engenharia – Estática e Quase Estática. 4 ed. Florianópolis: Editora UFSC, 2019. 397 p. ISBN 978-8532808295.

[6] BASTOS, João P. A.; SADOWSKI, Nelson. Electromagnetic Modeling by Finite Element Methods. 1. ed. [S. l.]: CRC Press, 2003. 510 p. ISBN 978-0824742690.

[7] KITTEL, Charles. Physical Theory of Ferromagnetic Domains. Reviews of Modern Physics, [S. l.], ano 4, v. 21, p. 441-491, out. 1949. Disponível em: http://www.fisica.unlp.edu.ar/Members/sanchez/Ej2%20viejo/Kittel1949_RevModPhys_21_541.pdf. Acesso em: 18 ago. 2022.

[8] SOUZA, J. A.; JARDIM, R. F. Electrical transport in disordered andordered magnetic domains underpressures and magnetic ﬁelds. Journal of Physics D: Applied Physics, [S. l.], v. 42, n. 3, p. 1-4, 9 jan. 2009. DOI 10.1088/0022-3727/42/3/032006. Disponível em: https://www.researchgate.net/publication/230902630_Electrical_transport_in_disordered_and_ordered_magnetic_domains_under_pressures_and_magnetic_fields. Acesso em: 18 ago. 2022.

[9] BERTOTTI, G. General properties of power losses in soft ferromagnetic materials. IEEE Transactions on Magnetics, [S. l.], v. 24, n. 1, p. 621-630, jan. 1988. DOI 10.1109/20.43994. Disponível em: https://ieeexplore.ieee.org/document/43994. Acesso em 18 ago. 2022.

[10] SCHLEGEL, J. P.; BATISTELA, N. J.; SADOWSKI, N.; KUO-PENG, P.; BASTOS, J. P. A.; RIGONI, M.; DE ESPÍNDOLA, A. A.; DOKONAL, L. V. Testing Strategies to Evaluate Non-Oriented Electrical Steels Losses. Journal of Microwaves, Optoelectronics and Electromagnetic Applications, [S. l.], v. 11, n. 2, p. 304-315, 12 dez. 2012. DOI https://doi.org/10.1590/S2179-10742012000200008. Disponível em: https://www.scielo.br/j/jmoea/a/kF9tmfg7gSy6QFNfLffTZTS/. Acesso em: 18 ago. 2022.

[11] BROCKHAUS. Epstein Frame. [S. l.], 2022. Disponível em: https://www.brockhaus.com/measurements/products/softmagnetic/est-series/soft-coils/epstein/?lang=en. Acesso em: 18 ago. 2022.

[12] PADILHA, Juliano B.; KUO-PENG, Patrick; SADOWSKI, Nelson; BATISTELA, Nelson J. Emprego do Modelo Dinâmico de Histerese de Jiles-Atherton para a Representação de Laços de Histerese Experimentais. MOMAG 2016: 12º CBMag e 17º SBMO. Anais de Congresso. Porto Alegre, 2016.

[13] APERAM. Aços Elétricos de Grão Orientado e de Grão Não-Orientado, [S. l.], 30 jul. 2012. Disponível em: https://brasil.aperam.com/wp-content/uploads/2015/08/A%C3%A7os-El%C3%A9tricos-GO-e-GNO.pdf. Acesso em: 06 jun. 2022.