Taludes Estabilizados
por Retroanálise – Análise Crítica e Comparativa com Métodos de Equilíbro Limite
Stabilized slopes by back analysis - critical and comparative
analysis with limit equilibrium methods
Douglas Correia Moscateli 1,2  https://orcid.org/0000-0001-5683-714X
https://orcid.org/0000-0001-5683-714X
Nelson Henrique Joly 1  https://orcid.org/0000-0001-5433-8080
https://orcid.org/0000-0001-5433-8080
José Antônio Urroz Lopes 3  https://orcid.org/0000-0002-9866-1661
https://orcid.org/0000-0002-9866-1661
Vítor Pereira Faro 4  https://orcid.org/0000-0003-0001-5459
https://orcid.org/0000-0003-0001-5459
1 Mestre em Engenharia de Construção Civil -
Geotecnia, PPGECC – UFPR, Universidade Federal do Paraná, Curitiba, Paraná,
Brasil,
2 Oficial do Corpo de Engenheiros da Marinha do Brasil – Comando
do Sexto Distrito Naval, Ladário, Mato Grosso do Sul, Brasil,
3 Mestre em Geologia Ambiental, PPGG – UFPR, Universidade
Federal do Paraná, Curitiba, Paraná, Brasil,
4 Professor Adjunto D.Sc., Departamento de Construção Civil da
Universidade Federal do Paraná (UFPR), Curitiba, Paraná, Brasil.
E-mail do autor principal: Douglas
Correia Moscateli douglasmoscateli@gmail.com
Resumo

Este
artigo apresenta uma comparação entre os métodos usuais de análise de
estabilidade de taludes: Fellenius [1], Bishop Simplificado [2], Spencer [3] e Morgenstern &
Price [4], que utilizam parâmetros
de resistência obtidos de ensaios de laboratório, e o método teórico e prático
de estabilidade de taludes naturais, através do método de regressão
desenvolvido por Lopes [5], que procura estimar a estabilidade de taludes artificiais, a
partir dos parâmetros de resistência obtidos com o exame de cicatrizes de
escorregamentos naturais. Utilizou-se como estudo de caso, um talude rodoviário,
localizado na Serra do Mar paranaense, que foi reprojetado utilizando o referido
método de regressão. A comparação mostrou que utilizando parâmetros obtidos em laboratório,
o FS resultante do talude (2,1) apresentou-se muito superior ao que foi imposto
ao projeto (1,4) e muito próximo do obtido pelo método de regressão de
Morgenstern & Price (1,5), indicando tratar-se de um método supostamente
conservador, com FS igual a 1,3.
Palavras-Chave: Taludes; Parâmetros de Resistência; Método de Lopes; Método
de Regressão.
Abstract

This
article presents a comparison between the usual methods of slope stability
analysis: Fellenius [1], Bishop Simplified [2], Spencer [3] and Morgenstern
& Price [4], which use resistance parameters obtained from laboratory
tests, and the theoretical and practical method of natural slope stability,
through the regression method developed by Lopes [5], which tries to estimate
the stability of artificial slopes, based on the resistance parameters obtained
by examining natural slip scars. A road slope located in Serra do Mar, Paraná,
was used as a case study, which was redesigned using the regression method
previously mentioned. The comparison showed that, using parameters obtained in
laboratory, the FS resulting from the slope (2.1) was much higher than that
imposed on the project (1.4) and very close to that obtained by the Morgenstern
& Price (1.5) regression method, indicating that it is a supposedly
conservative method, with FS equal to 1.3.
Key-words: Slopes; Parameters of
Resistance; Lopes Method; Regression Method.
1.
Introdução
Os movimentos de massa que acontecem tanto em taludes de corte e aterro
quanto em encostas naturais, são ocasionados "por fatores que geram o
aumento das tensões cisalhantes (sobrecargas, cortes, erosões, vibrações, etc)
e/ou a redução da resistência dos solos (intemperismo, fissuramento,
amolgamento e aumento da tensão neutra) que constituem os mesmos." [6].
A aplicação da retroanálise para análises de estabilidade de encostas, vem
sendo bastante considerada no meio geotécnico, tanto que a consagrada USACE (Corpo
de Engenheiros do Exército dos Estados Unidos), menciona a possibilidade de sua
aplicação para avaliar deslizamentos de solos e rochas, com o intuito de
estimar as forças cisalhantes e os níveis piezométricos, além de aferir a
estabilidade [7].
Galeandro et al., usando penetrômetro de bolso, demostrou que camadas
argilosas espessas e aparentemente homogêneas são, na realidade, extremamente
heterogêneas e anisotrópicas e possuem propriedades variáveis causadas pela
ação de processos como deposição, diagênese e intemperismo. Os referidos autores
mencionaram que “O perfil de resistência do solo mostrou que a relevante
variabilidade da resistência do solo [...] era mais alta que o esperado [...]” [8].
Christaras et al. estudando dois escorregamentos em margas do Neogeno do
Golfo de Kapsali na Grécia, verificaram que essas margas, quando secas, parecem
duras e coesivas, mas quando molhadas, perdem, imediatamente sua coesão. Testes
de laboratório indicaram valores de f = 23,2°
para condições secas que levavam à obtenção de um FS entre 1,05 e 1,3. Os
estudos de regressão, então realizados, estimaram entretanto, f de 18° e c de 4 kPa que resultaram em um FS entre
0,993 e 0,998; o qual explicava a ocorrência dos escorregamentos. A conclusão
desses autores foi que “[...] o método de regressão produz resultados mais
realistas do que os originais de laboratório porque leva em consideração as
condições ocorrentes no momento da ruptura.” [9].
Baseado nesse contexto, este trabalho busca ressaltar a importância das
análises de estabilidade em encostas e, ainda, verificar a eficiência do método
de retroanálise aplicado ao talude estudado nesta pesquisa; metodologia que foi
desenvolvida por Lopes [5],
descrita e apresentada no 3° CBGE, em Itapema-SC e utilizada por Queiroz [10] para o desenvolvimento de ábacos
altura/inclinação dos taludes de uma ferrovia, descritos em sua Dissertação de
Mestrado e, do mesmo modo, Lopes o incluiu, também, em sua Dissertação de
Mestrado [11]. Fiori &
Carmigiani [12] incluíram o Método
(por eles denominado “Método de Lopes”), em seu livro texto de Mecânica dos
Solos e Moscateli [13] o discutiu em sua Dissertação de Mestrado. O Autor incluiu,
ainda, o Método em seu livro sobre encostas [14] e o apresentou no ENGGEO’2019, na
Turquia [15].
Por
fim, o objetivo do presente artigo é a realização de análises paramétricas de
estabilidade, em um talude já estabilizado pela metodologia de regressão
proposta por Lopes [5],
comparando-a com métodos analíticos tradicionais, simulados em um programa
computacional, tanto no que tange ao fator de segurança resultante, quanto aos
parâmetros de resistência geotécnica obtidos por diferentes critérios.
1.1. Estudo de Caso
A encosta considerada para este trabalho, localiza-se entre os municípios
de Morretes e Antonina, na Serra do Mar paranaense, mais precisamente na cidade
de Antonina, no km 19,8 da rodovia PR-408, conhecida também como Rodovia
Deputado Miguel Bufara.
Eventos pluviométricos extremos ocorridos entre os dias 10 e
11 de março de 2011, na região de Antonina e Morretes, particularmente na
porção conhecida como Serra do Mar, ocasionaram problemas de instabilidades em
encostas naturais e taludes de cortes e aterros, na rodovia PR-408, se
estendendo por cerca de 260 m ao longo dessa rodovia.
Como solução para reestabilização da encosta, a empresa
consultora (ENGEMIN) [16] propôs a retirada da porção inferior (soerguida) da ruptura, com a reestabelecimento
do greide de pavimentação em seu nível original, conjuntamente com o
retaludamento e drenagem do corte, adotando-se um talude padrão compatível com
as características mecânicas que o material, ao que tudo indica, apresentou por
ocasião da ruptura e com a geometria da encosta, sendo, para tal, adotada a
metodologia desenvolvida por Lopes [5].
2. Métodos expeditos/empíricos
de retroanálise
Os dois subitens abaixo, tem por objetivo explanar duas
metodologias para retroanálise de taludes: o primeiro deles (Método de Hoek) [17] foi a base dos estudos que
originaram o segundo (Método de Lopes) [5], empregado como a principal ferramenta de análise
desta pesquisa.
2.1 Método de Hoek
O método proposto por Hoek [17], considera basicamente dois tipos de
ruptura: a planar, que ocorre ao longo de feições estruturais bem definidas,
como fraturas, falhas ou planos de acamamentos, e a circular ou rotacional, que
ocorre em locais de solos e rochas brandas, razoavelmente homogêneos
e que, como consequência, não têm suas propriedades mecânicas regidas por
feições estruturais. Além da condição “a seco”, o autor considera a possibilidade
de influência de pressão da água sob duas formas: “fluxo normal descendente, paralelo
ao talude, e fluxo horizontal, no qual o movimento livre descendente da água
subterrânea é inibido pela presença de camadas horizontais ou de juntas
argilosas impermeáveis.”. O método também considera a possibilidade de influências
de possíveis fendas de tração, saturadas ou secas [12].
Para o caso de ruptura circular (que foi o
adotado no estudo de caso desta pesquisa), os grupos adimensionais adotados por
Hoek [17], por fornecerem uma boa
aproximação à função ideal, foram os abaixo:
X = i – 1,2 f
(1)
Y = (gnat
H)/c (2)
onde:
X = função que define o ângulo de talude;
Y = função que define a altura de talude;
i = ângulo de inclinação do talude;
f = ângulo de atrito interno do solo;
gnat = densidade aparente
natural do solo;
H = altura do talude; e
c = coesão do solo.
O primeiro grupo foi denominado por Hoek [17] “função ângulo de
talude”, ou simplesmente X, e o segundo denominado “função altura do talude”,
ou Y. “Os valores da função X, quando plotados contra os da função Y, caem
sobre uma curva singular, que pode ser agora usada como base para um ábaco, uma
vez que, conhecendo-se um valor de X, o valor para a função Y= ɣH/c poderá ser obtido, e
vice-versa.”.
As relações estabelecidas por Hoek [17] entre os parâmetros
básicos de coesão e ângulo de atrito, e as duas funções X e Y, são de caráter
aproximado. Essas funções foram sendo ajustadas por tentativas e seus
resultados foram comparados com os obtidos utilizando-se os métodos
tradicionais, até obter-se boa concordância. Com elas o referido
autor desenhou o ábaco (Figura 1), cuja validade foi testada e confrontada com
métodos usuais de estudo de estabilidade.
A partir dos dois grupos originais,
representativos da condição “a seco”, Hoeck [17] introduziu correções para apresença de água
e fendas de tração, configurando seis situações (Figura 2), que possibilitam
nove combinações das
funções X e Y que, aparentemente, são suficientes para cobrir os casos mais importantes
que poderão surgir na análise da estabilidade de taludes em potencial de
ruptura.
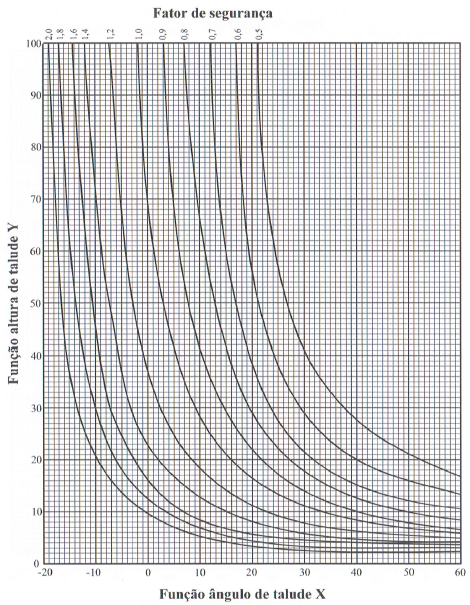
Figura 1: Ábaco de projeto de ruptura circular.
Fonte: Hoek (1972).
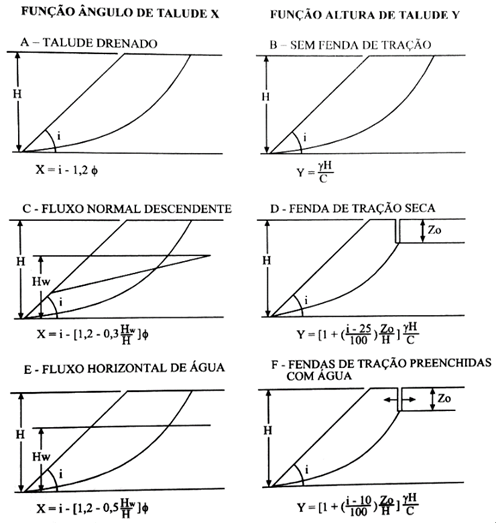
Figura 2: Funções X e Y para o acompanhamento do ábaco de ruptura
circular.
Fonte: Hoek
(1972).
onde:
X = função que define o ângulo de talude;
Y = função que define a altura de talude;
i = ângulo de inclinação do talude;
f = ângulo de atrito interno do solo;
g = densidade aparente natural do solo;
H = altura do talude;
HW = altura do nível d’água;
Zo = profundidade da fenda de tração; e
C = coesão do solo.
2.2 Método de Lopes
De acordo com Queiroz e Gaioto [17], fundamentado no
ábaco de ruptura circular proposto por Hoek [17], Lopes [5] desenvolveu um método de
estabilidade de taludes, que se baseia na observação de rupturas em encostas
naturais ou taludes artificiais, como ensaio em escala natural.
Seguindo a premissa do raciocínio de Lopes, este afirma que:
“a natureza como laboratório é insubstituível, e que os eventuais erros
introduzidos pela observação e hipóteses de trabalho não são maiores do que os
costumeiramente introduzidos pela relação de escalas entre os ensaios e a
realidade física e entre esta e as abstrações matemáticas.” [5].
O método busca a obtenção de parâmetros médios de
resistência (c e f), a partir de estudos de
regressão em cicatrizes de escorregamentos naturais, de mesma formação
geológica baseando-se, nesse estudo, nas premissas estabelecidas por Hoek [17]. Tal método pode ser
usado em anteprojeto como sugestão, não substituindo uma completa e rigorosa
investigação geotécnica, ou como indicação preliminar para composição de
orçamento. A ideia
consiste basicamente em estimar taludes artificiais com alturas e ângulos de
inclinações tais que apresentem condições de “estabilidade satisfatória”, isto
é, cujo fatores de segurança sejam no mínimo iguais aos que regem os taludes de
escorregamentos naturais [5].
Para a análise de estabilidade dos taludes, o mesmo autor
ainda parte de alguns princípios: (i) na assunção de que as superfícies de
escorregamento representam uma situação limite entre o estável (que permaneceu)
e o instável (que escorregou), ou seja, utilizando-se o linguajar usual da
Mecânica dos Solos, elas possuem fator de segurança muito próximo da unidade
uma vez que alguma coisa só escorrega, porque está instável e só para de
escorregar porque atingiu a estabilidade e (ii) na validade das relações
estabelecidas por Hoek [17].
A aplicação do método inicia-se por análises de imagens
aéreas do local, com o intuito de detectar-se as cicatrizes de escorregamentos existentes.
Uma vez localizadas as cicatrizes, a partir das informações obtidas das curvas
de nível oriundas de restituições aerofotográficas ou de levantamentos
topográficos, traçam-se os perfis longitudinais principais dessas cicatrizes,
invertendo-se-as de tal modo que tenham como origem comum o ponto mais alto de
cada uma delas. Na Figura 3 é traçada a envoltória dessas seções, onde podem
ser escolhidos os possíveis ângulos de taludes nela inscritos:
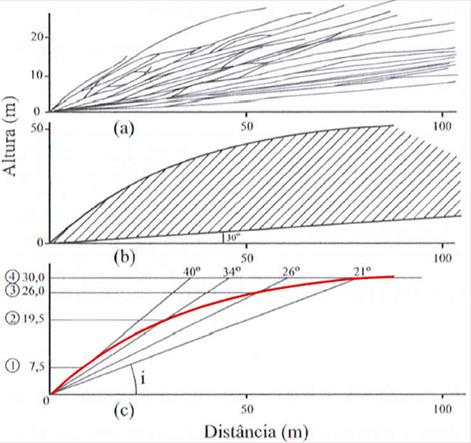
Figura 3: Ângulos de taludes e a curva envoltória.
Fonte: Lopes (1981).
De acordo com Lopes, a outra fase do estudo se resume a
vistoria(s) de campo. Esta(s) visa(m) obter caraterísticas mais detalhadas dos
locais das cicatrizes, o tipo de solo que constitui a vertente, condições
hidrogeológicas, entre outros aspectos considerados característicos e
importantes do local de estudo [5].
O autor do método ainda se baseia em determinadas observações
que estabelecem as hipóteses de como se supõe terem ocorrido as rupturas: o
grau de meteorização e pedogenização do material envolvido, a presença ou
ausência e a posição do lençol freático e a probabilidade de ocorrência de
fendas de tração e de seu preenchimento por água.
Depois do retorno do campo é identificada a hipótese mais
provável da ruptura, ou seja, o motivo pelo qual, aparentemente, a
vertente escorregou e sua forma: ruptura plana ou circular.
De posse das observações de campo, são estas comparadas às
situações representadas na Figura 2, devendo-se então selecionar o par de
equações X e Y mais adequado às condiçções do escorregamento. Escolhidas as
duas funções, substitui-se os pares de valores altura/ângulo limite dos taludes
escolhidos e estima-se o valor do peso específico do solo (ɣnat), que irão permitir o
estabelecimento de um certo número de equações numéricas possíveis [5].
Nos parágrafos abaixo está sintetizada a técnica de estimativa por regressão, desenvolvida
por Lopes [5]
a
partir da metodologia de estimativa de estabilidade proposta por Hoek [17] no formato de tópicos, os
quais descrevem as etapas de sua aplicação prática na encosta estudada,
produzindo um passo a passo, síntese do artigo original, e possível de
reprodução por demais autores que venham a estudar o método. Cabe ainda
ressaltar, que as etapas abaixo foram aplicadas desse mesmo modo, pelos
técnicos responsáveis pelo projeto de estabilização, no estudo de caso
apresentado neste artigo.
1) O projeto de retaludamento da encosta teve início com levantamentos
planialtimétricos realizados no local do escorregamento pouco tempo após os
eventos. Com os dados dessa topografia foi possível construir um mapa com
curvas de nível sobre o qual foram marcadas e analisadas as cicatrizes de
escorregamentos existentes e, a seguir, desenhadas as seções principais dessas
mesmas cicatrizes (invertidas), tendo como ponto comum, na origem, o seu ápice,
conforme ilustrado na Figura 3;
2) Após isto, pôde ser desenhada a curva envoltória de todas
as cicatrizes, onde foram escolhidos alguns ângulos de taludes caraterísticos
que a interceptavam, dando-se preferência àqueles mais usualmente empregados na
fase de construção e considerando-se que valores inteiros facilitam no
tabelamento das funções, ao mesmo tempo que era realizado, o registro da
inclinação (i) e altura (H) de cada talude estabelecido;
3) Realizado esse procedimento, os técnicos responsáveis pelo
projeto retornaram ao local do escorregamento com o intuito de estabelecer as
prováveis condições que deflagraram o processo do rompimento;
4) Estabelecidas as hipóteses mais prováveis que causaram as
rupturas, o próximo passo consistiu na escolha dos pares de funções X e Y
(Figura 2), dentre as estabelecidas por Hoek [17], nas quais foram substituidos os pares de
valores (inclinação/altura) encontrados na etapa 2 e o peso específico dos
solos (ɣnat) obtido por meio dos ensaios laboratoriais;
5) A seguir, variando-se, o valor do ângulo de atrito
dentro do intervalo
de validade (10º a 40°), estabelecido por Hoek [17] e calculando-se os valores da
função X correspondente, pôde-se, sobre a curva: Fator de Segurança (FS) = 1,0
do ábaco de Hoek (Figura 1) determinar os correspondentes valores da função Y
e, uma vez de posse
dos valores dessa função, calcularam-se os valores da coesão (c) que
satisfaziam as condições impostas pelos taludes escolhidos;
6) De posse dos diversos pares c/f possíveis,
foram então desenhados gráficos que resultaram em curvas que se interceptavam em
dois ou mais locais, indicando pares que atendiam simultâneamente a mais de um
par, indicando valores próximos dos mobilizados durante a ruptura da encosta;
7) Examinaram-se, então, as regiões dos interceptos, substituindo
os possíveis pares (c e f) nas funções X e Y que lhes
deram origem e, sobre o ábaco de Hoek, fazendo o caminho inverso da etapa 5, buscou-se
o FS do talude correspondente, mais próximo da unidade;
8) Estabelecido o par de parâmetros
representativo do momento da ruptura e, considerando ângulos de inclinação
usuais em construção de cortes com fatores de segurança desejados,
estabeleceram-se as alturas máximas de construção, a partir das funções X e Y,
previstas para taludes drenados, de vez que eram previstos drenos
subhorizontais nos taludes.
3.
Materiais e métodos
Para auxiliar o desenvolvimento deste trabalho, foram necessários além
dos diversos dados fornecidos pela empresa consultora do projeto de
estabilização [16],
referente ao estudo de caso, alguns ensaios e coletas complementares, para que
então fossem possíveis as diversas análises e comparações objetivadas pelos autores deste
artigo.
A metodologia do trabalho seguiu as etapas abaixo
resumidas:
1) Levantamento de dados topográficos, geológicos e geotécnicos dos
taludes estudados e históricos das movimentações, contidos em relatórios
técnicos cedidos pela empresa consultora;
2) Coleta de amostra indeformada em campo para subsidiar os ensaios, e
com os resultados obtidos, complementar os parâmetros aplicados na etapa de
análises de estabilidade;
3) Realização
de ensaios de
cisalhamento direto para obtenção dos parâmetros de resistência do solo: coesão
(c) e ângulo de atrito (f);
4) Estudo e investigação do Método de Lopes [5] e de Hoek [17], na obtenção dos parâmetros de resistência do solo, aplicados no estudo
de caso, junto ao próprio autor do método, o MSc. José Antônio Urroz Lopes e suas
publicações ([5], [11], [14], [15]), como também em bibliografias consagradas que tratam do tema: p. ex. Deere
& Patton [19], Hoek
[17], Sir Benjamin Baker (1881),
transcrito por Spanger & Hardy [20], Fiori & Carmigiani [12], bem como por outros conhecidos autores da Mecânica dos Solos
como Terzaghi & Peck [21], Taylor [22] e
Lambe & Whitman [23].
5) Estimativa por retroanálise, utilizando um programa de análise de
estabilidade do tipo equilíbrio limite: software Slope/W (Geo-Slope
International, 2007, versão 07), dos parâmetros de resistência ao cisalhamento
do solo, adotando-se o método clássico e rigoroso de Morgenstern e Price [4];
6) Simulação paramétrica de estabilidade com o software Slope/W, para a
obtenção do fator de segurança dos taludes já dimensionados pela consultora
(retaludados), aplicando os parâmetros obtidos no estudo de retroanálise por
Morgenstern e Price [4];
7) Simulação paramétrica de estabilidade com o software Slope/W, para a
obtenção do fator de segurança dos taludes já dimensionados pela consultora
(retaludados), aplicando os parâmetros obtidos por meio de ensaios canônicos de
laboratório;
8) Simulação paramétrica de estabilidade com o software Slope/W, para a
obtenção do fator de segurança dos taludes já dimensionados pela consultora
(retaludados), aplicando os parâmetros obtidos no estudo de regressão de Lopes [5];
9) Comparação e análise crítica dos resultados dos fatores de segurança
(FS) obtidos nas etapas anteriores, com ênfase para a metodologia proposta por
Lopes [5] e comparações entre esta e as demais metodologias.
4.
Apresentação
dos resultados
Este item aborda os resultados dos parâmetros de resistência ao
cisalhamento dos solos, o intercepto coesivo (c) e ângulo de atrito (f), obtidos por intermédio das metodologias aplicadas
neste trabalho. Os referidos parâmetros foram aplicados comparativamente nas
análises determinísticas tradicionais de estabilidade, apresentadas no item 4.5.
4.1. Ensaios laboratoriais
Os ensaios de resistência ao cisalhamento direto obtiveram parâmetros de
resistência para as condições de pico (na ruptura). Realizados os ensaios, foi
possível definir a envoltória de ruptura em termos de tensões efetivas. Os resultados
obtidos para os parâmetros, apresentaram para a coesão o valor de 18,4 kPa, e para
o ângulo de atrito: 30º.
4.2. Obtenção dos parâmetros
por correlações
Em razão da dificuldade de se escavar o talude a profundidades superiores
a 1,5 metros, somente foi feita a coleta de amostras indeformadas na primeira
camada, próxima a superfície e, consequentemente, só foi possível caracterizar
os parâmetros de resistência desse primeiro horizonte de solo. Em razão desse
fato, e para suprir esta deficiência, foi adotada neste trabalho, uma estimativa
dos parâmetros geotécnicos, efetuada através de correlações entre o índice de
resistência à penetração (NSPT) e os
parâmetros de resistência ao cisalhamento do solo, disponíveis na literatura técnica.
O talude do estudo de caso em questão, apresentou na camada inferior, um solo composto
por silte muito arenoso e com pouca argila, variando de 4 a 14 metros
aproximadamente, conforme ilustrado na sondagem geotécnica da Figura 4 e no
perfil geotécnico da Figura 8.
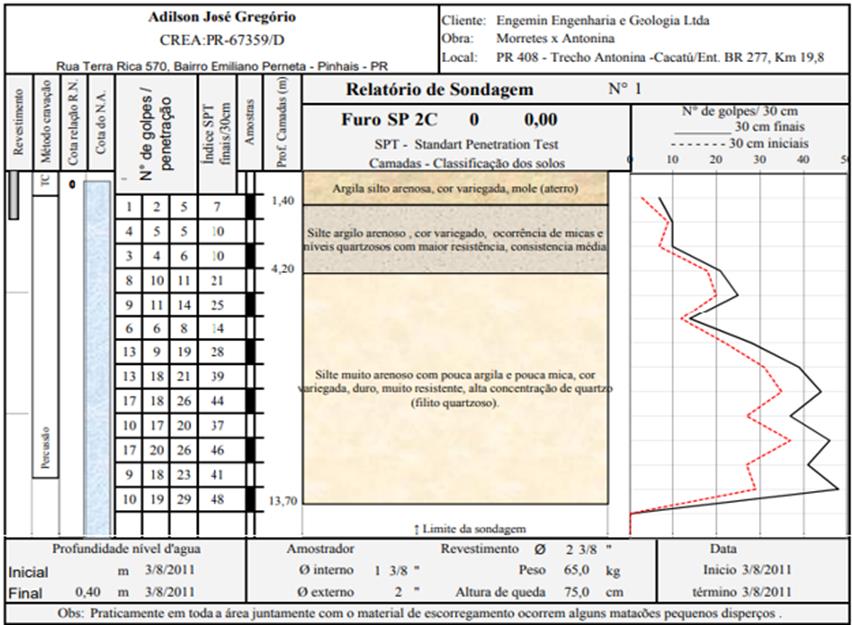
Figura 4: Sondagem geotécnica do estudo de caso, com a descrição
dos tipos de solos residuais.
Fonte: ENGEMIN (2011).
Para a estimativa do ângulo de atrito na camada do Solo Residual B, foram
utilizadas e comparadas duas correlações.
A primeira proposta por TEIXEIRA (1996), apud Cintra [24]:
f=√(20.Nspt)+15° (3)
A segunda proposta por BOWLES (1996), apud Tonus [25]:
f=0,45 (N70)+20 (4)
Onde:
N70=((Nspt.Energia aplicada))/0,70
(5)
Aplicando nas equações, o NSPT
médio da camada no valor de 34,3 golpes / 0,3 m, e o valor de 0,66
correspondente a 66% da energia teórica de queda livre aplicada durante o
ensaio, de acordo com Schnaid [26], obteve-se como resultado um ângulo de atrito igual à 41°
para a correlação de Teixeira (1996) e de 34° para a de Bowles (1996), ambos
dentro do intervalo característico para material arenoso. Foi adotado nos
estudos de estabilidade desta pesquisa, o menor desses valores, procurando-se
dessa forma, trabalhar com um cenário mais pessimista e conservador.
Para a
estimativa da coesão (c) e do peso específico natural (ɣnat), o autor principal buscou valores na literatura, a qual
considera ensaios em solos representativos da mesma região, sendo, por isso,
adotados valores ligeiramente superiores aos encontrados nos ensaios da primeira
camada (Solo Residual A), procurando manter-se um conservadorismo na estimativa
e uma equivalência com dados reais de ensaios. O Quadro 1 resume os parâmetros
estimados e adotados para a camada do Solo Residual B referente ao estudo de
caso.
Quadro 1: Resumo dos parâmetros obtidos por correlações e na literatura para o
solo residual B (Antonina - PR)

Fonte: Moscateli (2017) [13].
4.3.
Retroanálise
Morgenstern e Price (1965)
Conforme descrito no item 3 - Materiais e Métodos, foi necessário o
levantamento de informações para a entrada de dados no modelo de retroanálise
aplicado ao software Slope/W. Estas foram obtidas dos levantamentos
topográficos fornecidos pela empresa consultora e de observações diretas feitas
nos locais que permitiram reconstituir a geometria inicial das encostas: aquela
imediatamente anterior ao escorregamento de Antonina.
No que tange à condição da pressão neutra no interior do maciço, foi
adotada uma linha piezométrica localizada a meia altura da encosta, ou seja,
considerando esta última numa condição próxima da saturada, em razão do
encharcamento do solo causado pelos intensos eventos pluviométricos e pela
ausência de dispositivos de drenagem, situação esta, considerada a mais
provável, por ocasião da deflagração dos escorregamentos.
Seguindo a metodologia proposta no item 3 (etapa 5), com o
objetivo de estimar os parâmetros médios equivalentes de resistência do talude
natural que mais próximos representaram a resistência média no momento da
ruptura, partiu-se do trabalho feito por Tonus [25], à qual realizou análises em
uma encosta próxima à região de estudo desta
pesquisa, com características geológico-geotécnicas da região da Serra do Mar
paranaense, e que apresentou sinais de instabilidades passando por obras de
estabilização.
Após serem realizadas diversas iterações e ajustes no modelo,
fundamentado em Dell’Avanzi
et al. [27], o qual produziu um trabalho onde
reúne valores de parâmetros de resistência publicados pelo próprio autor e por
Suzuki (2004) em conferências e relatórios técnicos, referente a ensaios de
cisalhamento direto e triaxial drenado, de solos residuais originados de rochas
de Migmatito; pôde-se
chegar a um satisfatório ajuste da superfície de ruptura e do fator de
segurança unitário (FS = 1,039), que representariam a iminência do
deslizamento, obtendo-se assim, os menores valores médios dos parâmetros de
resistência que levariam ao colapso do maciço: c = 9,8 KPa e f = 26° para a camada A de solo
residual e c = 10,5 KPa e f = 28° para a camada B de solo residual, valores esses,
bastantes próximos e contido no intervalo apresentado por outros autores na
literatura e nos ensaios de laboratório desta pesquisa.
4.4.
Retroanálise
Lopes (1981)
Seguindo as etapas 1 e 2 do passo a passo do método (item 2.2), foram sobrepostos
os perfis levantados a partir das cicatrizes do escorregamento, no trecho em
estudo, onde foi possível delimitar a envoltória característica dessas
cicatrizes (Figura 5) e os possíveis taludes que a interceptam (Figura 6).
Foram determinados cinco segmentos de taludes cujos ângulos escolhidos e
alturas máximas correspondentes foram os seguintes:
i = 43° H = 12,48 m
i = 38° H = 15,67 m
i = 31° H = 19,47 m
i = 27° H = 24,32 m
i = 25° H = 27,35 m
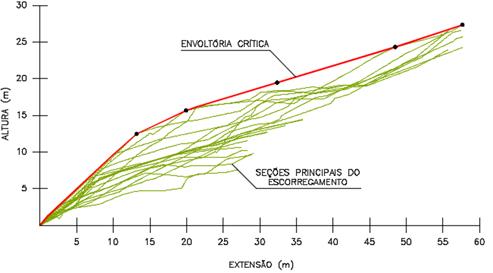
Figura 5: Sobreposição das cicatrizes de escorregamento e delimitação
da envoltória característica.
Fonte: Adaptado
de ENGEMIN (2011).
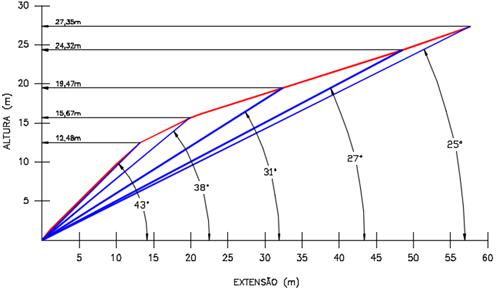
Figura 6: Escolha dos taludes limites e seus respectivos pares de
inclinação e altura.
Fonte: Adaptado
de ENGEMIN (2011).
Seguindo a etapa 3 e 4 do mesmo item, por se tratar de movimentos
recentes, foi relativamente fácil estabelecer as condições em que ocorreram as
rupturas.
Dentre os condicionamentos ambientais
propostos por Hoek [17] (Figura 2), todas as evidências de campo acerca das condições em
que ocorreram as rupturas, indicaram a elevação da pressão neutra pelo excesso
de chuva, o que permitiu descartar o cenário com taludes drenados e presumir-se o não desenvolvimento
de fendas de tração.
Com base nesses fatos, foram definidas as
variáveis para os valores numéricos das funções e o estabelecimento das
hipóteses para execução dos cálculos, que foram as seguintes:
·
Situação
de estabilidade dos taludes resultantes de escorregamentos (Fs ≈ 1);
·
Presença
de nível d’água à meia altura dos cortes (HW/H = 0,5);
·
Validade
de utilização de “parâmetros equivalentes médios” ao longo dos cortes;
·
Peso
específico do solo em estado natural, obtido por estimativa: ɣnat = 2,00 g/cm³.
Substituindo então, nas funções de cada um dos taludes
adotados, as variáveis estabelecidas, pelos valores numéricos, foram obtidas
duas combinações de equações para cada possibilidade de talude presente no
estudo de caso.
Dando continuidade ao processo de cálculo, (etapa
5), foram atribuídos valores na faixa de 10° a 40° para a variável ângulo de
atrito, correspondente à função ângulo de talude (X), para cada um dos taludes,
onde foi possível
determinar seus respectivos valores.
Após obter-se os valores para as funções ângulo de
talude (X),
pôde-se no ábaco de Hoek [17] (Figura 1), sobre a curva FS = 1,0, por estar buscando
parâmetros do momento de ruptura, determinar os valores de Y, que, por sua vez,
forneceram os valores de coesão.
O passo seguinte consistiu na colocação, em gráfico, dos
diversos pares c/f passíveis de atenderem às condições impostas por cada talude-limite e em
verificar-se regiões de intersecções entre dois ou mais deles, uma vez que,
nessas regiões deveriam situar-se os pares que atendem às condições dos
diversos taludes parciais.
A título de exemplo, o Quadro 2 e a Figura 7, demonstram
respectivamente: a planilha contendo os diversos pares de parâmetros obtidos
por intermédio de iteração do método e, o respectivo gráfico com as curvas
correspondentes de cada talude.
Quadro 2: Possíveis
pares de parâmetros (c/f) para o cenário: Talude com fluxo normal descendente e sem
fenda de tração)
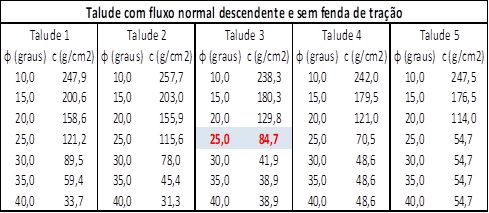
Fonte: Moscateli
(2017).



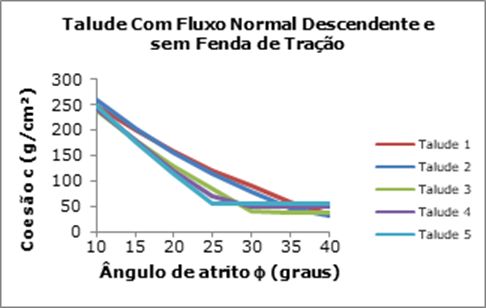
Figura 7: Gráfico: (c x f) para taludes com fluxo normal
descendente e sem fenda de tração.
Fonte: ENGEMIN (2011).
Com os diversos pares c/f colocados no gráfico,
seguindo a instrução da etapa 7 e considerando a região de intercepto das
curvas no gráfico, calculou-se o fator de segurança para cada um dos taludes
escolhidos, buscando-se chegar ao par que melhor atende às condições impostas
por todos os taludes, e que é aquele para o qual todos eles se aproximaram do
FS = 1,0, valor do qual, também, se aproximou a média geral dos FS individuais
de todos os taludes parciais.
O Quadro 3 apresenta alguns dos pares
obtidos nos interceptos, cujo exame mostra claramente que o intercepto B é o que melhor satisfaz
às condições impostas pelas rupturas totais, sendo portanto, admitida como
representativa: a ruptura com fluxo normal descendente e sem fenda de tração, e
adotados os valores dela obtidos: f = 25° e c = 85 g/cm2.
Quadro 3: Cálculo dos coeficientes de segurança para cada
talude escolhido nos interceptos
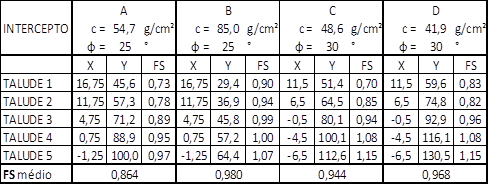
Fonte: ENGEMIN (2011).
onde:
X = função que define o ângulo de talude;
Y = função que define a altura de talude;
FS =
fator de segurança do talude;
f = ângulo de atrito interno do
solo;
c =
coesão do solo.
Cumprindo a última etapa (8), foram
selecionados os parâmetros considerados representativos da ruptura e, utilizando-se ângulos de
inclinação usuais em construção de cortes, estabeleceram-se as alturas máximas
passíveis de serem construídas e que, trabalhando a seco (isto é, utilizando
sistemas de drenagem), mantivessem fatores de segurança de 1,1; 1,2; 1,3; 1,4 e
1,5, respectivamente. A Tabela 1 mostra a determinação das alturas máximas
permitidas para cada segmento de talude, a partir da adoção dos parâmetros
representativos e das funções estabelecidas para taludes drenados e sem fenda
de tração.
Tabela 1: Alturas máximas possíveis de construção de taludes para cada ângulo e
fator de segurança determinado
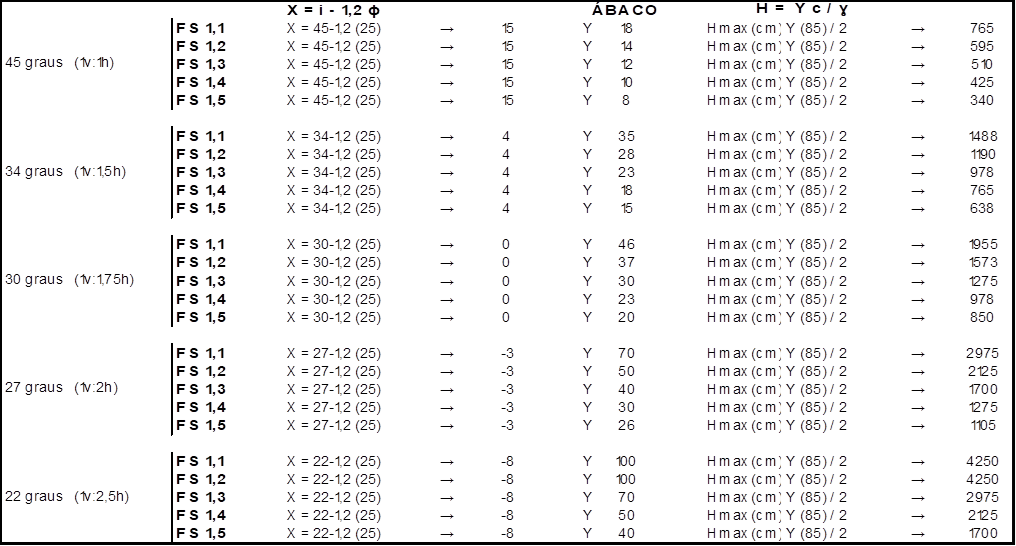
Fonte: ENGEMIN
(2011).
Por outro lado, para atender as
determinações da NBR 11682/2009, o projeto impôs um fator de segurança igual à
1,4 para os taludes, uma vez que esse talude ainda que não estivesse localizado
em uma região que continha áreas urbanizadas nem edificações nas proximidades
(as que existiam foram desapropriadas), a rodovia em questão possui um tráfego
intenso devido ao considerável fluxo turístico da região e das cidades de
Antonina e Morretes que se ligam por essa rodovia.
Além disso, por se tratar de um local
crítico - a Serra do Mar Paranaense, caracterizada por deslizamentos durante
períodos de chuvas intensas e, mais ainda, devido ao grande histórico de
instabilidades nas proximidades, a empresa projetista considerou necessário adotar
essa segurança de 40 % sobre a condição geral dos taludes que se mantiveram
incólumes.
O talude tipo (Figura 8) resultou da
combinação conveniente de taludes nominais e banquetas intermediárias, de modo
que as alturas de cada segmento, em nenhum ponto ultrapassassem as alturas
máximas calculadas para cada inclinação nominal, mantendo-se um fator de
segurança de 1,4.
Assim, o mesmo consta de segmentos com
alturas máximas de 7 m e inclinações variáveis: a inferior e intermediária, de
1 v : 1,75 h; e superior, de 1 v : 1,50 h. Entre esses segmentos foram
previstas banquetas com largura de 4,00 m, que além de permitirem o tráfego de
equipamentos de construção, são necessárias à construção de sarjetas para águas
superficiais e de drenos profundos para rebaixamento do lençol freático, além
de servirem como anteparos para eventuais instabilidades localizadas.
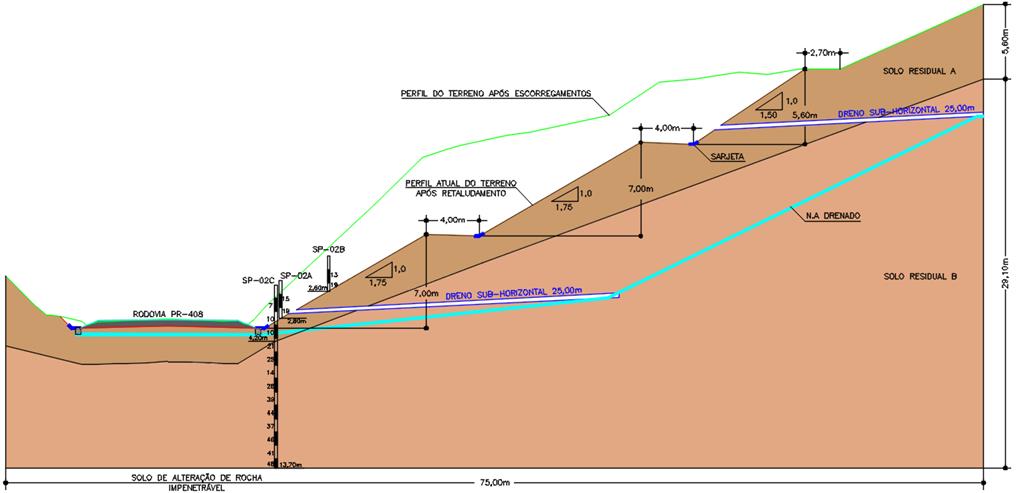
Figura 8: Perfil geotécnico com a solução de retaludamento e drenagem.
Fonte: Adaptado
de ENGEMIN (2011).
4.5.
Comparação
analítica do fator de segurança e dos parâmetros geotécnicos
Foram executadas 36 determinações de FS para
o talude constante da Figura 8, variando-se os métodos de análise, a condição
do NA e o par de parâmetros adotados em cada caso. O Quadro 4 resume os métodos
de obtenção e os pares de valores que foram aplicados nas diferentes análises.
Quadro 4: Resumo dos pares de
parâmetros geotécnicos aplicados nas análises de estabilidade

Fonte: Moscateli (2017).
O Quadro 5 resume os resultados dos fatores
de segurança obtidos nas análises determinísticas. Verifiou-se, nas análises
feitas no Slope/W, que existe uma semelhança evidente entre os métodos clássicos, os quais
apresentaram resultados de FS e superfícies de ruptura, muito próximos entre
si, com exceção do Método de Fellenius, que registrou valores sensivelmente
menores que os demais para as condições NA no topo e à meia altura do talude.
Como o principal objetivo deste trabalho é analisar a eficiência da
retroanálise proposta por Lopes [5], por meio do exame dos taludes projetados por esse
método, o autor principal achou por efeito prático, analisar a média dos FS obtidos nos
métodos clássicos (Quadro 5), em comparação com premissas normativas e também
com o FS = 1,1, estipulado pelo próprio Método de Lopes, verificando se tal FS
é equivalente àqueles mais tradicionais.
Quadro 5: Resumo
dos resultados dos FS obtidos nas análises determinísticas
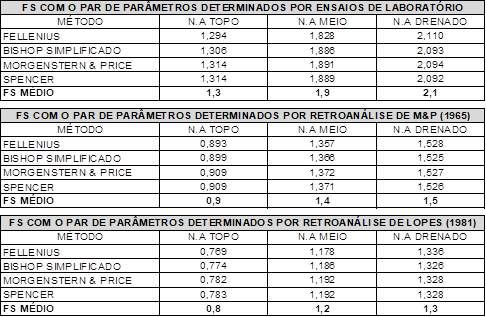
Fonte: Moscateli (2017).
Conforme mostra o Quadro 5, o FS = 1,3
obtido utilizando-se os parâmetros estimados pelo Método de Lopes, para o
talude drenado, corresponde a um FS = 1,5 utilizando-se os parâmetros obtidos
da retroanálise de Morgenstern & Price e 2,1, utilizando-se os parâmetros
de laboratório, o que significa que o FS da exigência da NBR 11682/2009 (1,4)
está perfeitamente coberto, assegurando, teoricamente, a estabilidade do talude
e confirmando novamente o aparente conservadorismo do método em questão.
Analisando a situação intermediária, foi
verificado que: com os parâmetros de Lopes, o FS estaria considerando 20 % de
segurança, mantendo uma condição de estabilidade. Como já foi descrito
anteriormente, por se tratar de um método de estimativas conservadoras,
verificou-se nas análises com a aplicação dos parâmetros de laboratório e de
Morgenstern e Price, o registro de um FS superior: de 1,9 e 1,4,
respectivamente, mostrando que: mesmo em uma situação agressiva, diferentemente
da condição normal prevista em projeto, com os sistemas de drenagem mantendo o
NA rebaixado, os taludes ainda assim, estariam com um elevado fator de
segurança, acima até mesmo do indicado por norma.
Na condição mais crítica considerada para o
excesso de pressão neutra agindo nos taludes, a partir da aplicação no modelo
de análise, dos parâmetros obtidos por Lopes e Morgenstern e Price, ambos de
processo de retroanálise, o valor do FS ficou abaixo da unidade, notando-se
que: quanto mais próximo da superfície do talude o nível d’água se encontrar,
mais se reduz o FS. Em contrapartida, evidenciando o conservadorismo do método,
os parâmetros obtidos por ensaios de laboratório registraram um FS = 1,3 que,
apesar de representar uma condição de segurança bastante satisfatória em uma
situação extrema de condições impostas ao talude, recai naquela mesma ideia
apontada por Lopes, de que nada adiantaria esse FS mantenedor da estabilidade
numa condição dessas, se ao entorno as encostas adjacentes já teriam sido
desestabilizadas.
5.
Conclusões
O método de regressão evidenciado neste trabalho, é bastante
válido e aplicável para casos de obras lineares, que compõe uma das dimensões
do problema, relativamente maior que as demais, dispondo-se de grande
variabilidade geotécnica. A regressão obtém os parâmetros de resistência, a
partir de dados reais da encosta (topografia, regime geohidrológico etc.), os
quais consideram as condições de contorno em escala natural, presumindo o
efeito da heterogeneidade. No entanto, considera-se imprescindível a execução
de investigações geotécnicas e ensaios laboratoriais, bem sucedidos, e em
quantidades satisfatórias, calibrando e comparando os modelos de retroanálise
com os métodos tradicionais, afinal, a importância da boa estimativa dos
parâmetros, é um fator crítico e fundamental nos resultados finais de projetos.
Complementando a ideia do parágrafo anterior, cabe ressaltar,
a partir de conclusões já feitas por Lopes [5] em seu artigo, citando e mantendo a
linha de raciocínio de Hoek [17] e que os autores desta pesquisa também acompanham,
que: o método de estimativa de estabilidade de taludes artificiais, a partir do
exame de cicatrizes de escorregamentos naturais “não pretende substituir os
métodos de projeto de talude mais sofisticados e mais precisos, os quais
deveriam ser aplicados quando a estabilidade de um talude é crítica e quando a
exatidão dos dados de entrada justifique a aplicação destes métodos”.
O trabalho apresentou o estudo de um só caso, contudo, observou-se
que os parâmetros obtidos por retroanálise, utilizando-se o Método de Lopes,
foram inferiores àqueles obtidos por ensaios canônicos de laboratório, apresentando
resultados relativamente conservadores.
Em relação aos valores obtidos pela
retroanálise feita pelo método de Morgenstern e Price, os valores foram
bastante próximos e coerentes, sendo, entretanto, os desta última, ainda
superiores.
Outro fator relevante analisado, foi a
comparação dos resultados em termos de fatores de segurança. Adotando FS
nominalmente inferiores aos da Norma, em razão da previsão do conservadorismo
dos parâmetros derivados do seu Método, Lopes obteve valor de FS = 1,3, muito
próximo dos prescritos por aquela (1,4), quando substituídos os parâmetros
obtidos pelo Método das Cicatrizes pelos obtidos pelos métodos tradicionais (que
são os considerados pela Norma), considerando-se o mesmo cenário.
Ficou evidenciada, desse modo que, da avaliação
de estabilidade, utilizando-se os parâmetros obtidos por ensaios de laboratório
e a partir da retroanálise de Morgenster e Price, resultaram fatores de
segurança superiores ao de Lopes e que, uma vez efetuadas as devidas
substituições obtiveram-se fatores de segurança que atendem ao preconizado pela
NBR 11682/2009, o que pressupõe que o talude estudado deve encontrar-se
estável.
Por fim, pôde-se concluir, que a metodologia
proposta e comparada nesta pesquisa, apresentou-se promissora na análise de
estabilidade de taludes, sendo aparentemente conservadora e de prática
aplicação.
6.
Agradecimentos
O primeiro autor deste artigo, Moscateli, agradece
honrosamente pelo respeito, a amizade, e ao compartilhamento dos conhecimentos,
repassados pelos orientadores do trabalho de dissertação que fundamentou a
produção deste artigo, os senhores: José Antônio Urroz Lopes e Vítor Pereira
Faro; agradecendo também, a inestimável contribuição de Nelson Henrique Joly no
desenvolvimento das análises de estabilidade, e por fim, os autores agradecem a
CAPES e ao Programa de Pós-Graduação em Engenharia de Construção Civil (PPGECC)
da Universidade Federal do Paraná, pelo apoio e viabilização desta pesquisa.
Referências
[1] FELLENIUS, W., “Calculation of the
Stability of Earth Dams.”, 2 nd International Congress on Large Darns,
International Commission on Large Dams, Washington, DC, 445-459, 1936.
[2] BISHOP, A. W., “The Use of the Slip
Circle in the Stability Analysis of Slopes”, Geotechnique, 5(1), 7- 17, 1955.
[3] SPENCER, E. A
method of analysis of the stability of embankments assuming parallel
inter-slice forces. Géotechnique, 17, pp. ll-26, 1967.
[4]
MORGENSTERN,
N. R.; PRICE, V. E. The analysis of the stability of general slip surfaces. Geotechnique, London, v.15, n.1, p.79 – 93, 1965.
[5] LOPES, J. A. U. Algumas
Considerações Sobre a Estabilidade de Taludes em Solos Residuais e Rochas
Sedimentares Subhorizontais. In: CBGE (CONGRESSO BRASILEIRO DE GEOLOGIA
E ENGENHARIA), 3th, 1981, Itapema-SC. Anais do 3° Congresso Brasileiro de
Engenharia e Geologia. Itapema: Associação Brasileira de Geologia de
Engenharia, v.3, p. 167-186, 1981.
[6] CAPPELLESSO, L. Retroanálise do Movimento de Massa do Talude localizado
na Rodovia Antônio - Criciúma SC. Artigo Científico do Curso de Engenharia
Civil, Universidade do Extremo Sul Catarinense, Criciúma, 2011.
[7] SESTREM, L. P.; DYMINSKI, A. S; KORMANN, A. C. M.; SANTOS, C. J. A. Retroanálise
de estabilidade de talude rodoviário em uma encosta litorânea em Santa
Catarina. In: COBRAMSEG 2012 - XVI Congr. Bras. de Mec. dos Solos e Eng.
Geotécnica, 2012, Porto de Galinhas. Anais do XVI COBRAMSEG. São Paulo: ABMS,
v. 1. p. 1-8, 2012.
[8] GALEANDRO, A; DOGLIONI, A; SIMEONE. Statistical Analyses of Inherent
Variability of Soil Streght and Effects on Engineering Geology Design. Bulletin
of Engineering Geology and the Environment. 76 (2): 587-600, 2017.
[9] CHRISTARAS, B; ARGYRIADIS, M;
MORAITI, E. Landslides in the Marly Slope of the Kapsali Area in Kithira Island
Greece. Bulletin of
Engineering Geology and the Environment. 73 (3): 839-844, 2014.
[10] QUEIROZ, R.C. Aplicação do Método de
Retroanálise no Estudo da Estabilidade de Taludes de Estradas Situadas em Solos
Oriundos da Formação Adamantina. M.Sc. tese, Escola de Engenharia de São
Carlos, Universidade de São Paulo, 274 p., 1986.
[11] LOPES, J. A. U. Os Movimentos
Coletivos dos Solos e a Evolução das Encostas Naturais nas Regiões Tropicais e
Subtropicais Úmidas. M.Sc. tese, Universidade Federal do Paraná, Curitiba –
Paraná, 157 p., 1995.
[12] FIORI, A. P; CARMIGNAMI, L. Fundamentos de mecânica dos
solos e das rochas: aplicações na estabilidade de taludes. 2.ed. Curitiba: UFPR,
2009.
[13] MOSCATELI. Taludes estabilizados por retroanálise –
Análise crítica e comparação com métodos tradicionais de análise de equilíbrio
limite. Dissertação de Mestrado. Universidade Federal do Paraná, Curitiba,
2017.
[14] LOPES, J. A. U. Encostas Evolução, Equilíbrio e
Condições de Ocupação. Porto Alegre: Alcance, 342 p., 2017.
[15]
LOPES, J. A.
U. National Symposium on Engineering Geology and Geotechnics ENGGEO’ 2019,
2019.
[16] ENGEMIN Engenharia e Geologia. Relatório do Projeto: Obra 608
- Ocorrências km 19,8. Pinhais-PR. Relatório técnico, 2011.
[17] HOEK, E. Estimando a Estabilidade de Taludes Escavados
em Minas a Céu Aberto. Tradução n. 4, APGA, São Paulo, 58p., 1972.
[18] QUEIROZ, R. C.; GAIOTO, N. Determinação
do Fator de Segurança em taludes de cortes ferroviários por retroanálise. In:
CONGRESSO BRASILEIRO DE GEOLOGIA DE ENGENHARIA, São Paulo: ABGE, p. 109-119,
1987.
[19]
DEERE, D. V.;
PATTON, F. D. Slope Stability in Residual Soil. Proceedings 4th Panamerican
Conference on Soil Mechanics and Foundation Engineering. San Juan, v.1, 87-170,
1970.
[20]
SPANGLER, M.
G.; HANDY, R. L. Soil Engineering (3rd ed.). New York: Intext International,
748 p., 1973.
[21] TERZAGHI, K; PECK, R. B. Soil Mechanics in
Engineering Practice (2nd ed.). New York: John Wiley & Sons, 566 p., 1966.
[22] TAYLOR, D. W. Fundamentals of Soil Mechanics
(2nd ed.). New York: John Wiley & Sons, 700 p., 1966.
[23]
LAMBE, T. W.;
WHITMAN, R. V. Soil Mechanics. New York: John Wiley & Sons, 553 p., 1979.
[24] CINTRA, J.; AOKI, N; ALBIERO, J. Fundações diretas:
projeto geotécnico. São Paulo: Editora Oficina de textos, 2011.
[25] TONUS, B. P. A. Estabilidade de taludes: avaliação dos
métodos de equilíbrio limite aplicados a uma encosta coluvionar e residual da
Serra do Mar Paranaense. Dissertação de Mestrado. Universidade Federal do
Paraná, Curitiba, 2009.
[26] SCHNAID, F.; ODEBRECHT, E. Ensaios de Campo e suas
aplicações à Engenharia de Fundações: 2ª edição. Oficina de Textos, 2012.
[27] DELL’AVANZI, E. e SILVA, D. P. Estabilidade de Encostas - Considerações
sobre a acurácia dos modelos de previsão da segurança. In: GeoSul 2013- IX
Simpósio de Prática de Engenharia Geotécnica da Região Sul, Cricíuma-SC,
Brasil, 9p. 2013.
https://orcid.org/0000-0001-5683-714X
https://orcid.org/0000-0001-5433-8080
https://orcid.org/0000-0002-9866-1661
https://orcid.org/0000-0003-0001-5459