1
Introdução
O desenvolvimento
do automóvel trouxe consigo várias vantagens para o transporte de cargas e
pessoas, porém, juntamente com esses benefícios vieram diversas questões de
segurança. Segundo Happian-Smith, o uso seguro e confiável de um veículo de
estrada necessita do contínuo ajuste de sua velocidade e distância em resposta
às mudanças de condição do tráfego [1]. O sistema de freio deve executar,
então, algumas tarefas essenciais durante todo o período de operação. Tais como
a desaceleração do veículo de forma controlada e repetível e, quando
apropriado, possibilitar a parada total do veículo, manter uma velocidade
constante quando percorrendo trechos em declive e manter o automóvel
estacionário, tanto em pisos na horizontal quanto em inclinações [2]. Essa capacidade de frenagem deve ser
averiguada mesmo a altas temperaturas, como é testado por Ishak et al. [3].
A compreensão
da dinâmica veicular pode ser realizada de duas formas, o método empírico e o
analítico. O entendimento empírico é baseado na tentativa e erro onde são
determinados quais fatores influenciam o desempenho do veículo [4]. Enquanto a formulação analítica
descreve as relações de interesse baseadas nas leis físicas, a fim de obter um
modelo matemático. Tal modelo fornece um meio de identificar os fatores mais
importantes, como operam e sob quais circunstâncias. Além disso, o modelo tem
capacidade de previsão, empregado para buscar um desempenho otimizado do
sistema e verificação em situações de emergência [5], ou implementado no controle de
sistemas autônomos.
Os modelos da
dinâmica veicular possuem diferentes abordagens, desde o tradicional modelo de
massas concentradas até o modelo de elementos finitos (FEM), e outras como o
modelo de subestrutura dinâmica e o modelo multicorpos com elementos não
lineares [6].
Porém, devido
a inúmeros fatores que agem sobre a frenagem de um veículo são necessárias
algumas simplificações nos modelos, o que os torna passíveis a erros. Portanto,
para a validação de tais modelos são necessários testes de campo a partir do
sistema de freio real [7]. Assim, em função da importância da
metodologia de validação e homologação de modelos numéricos à indústria
automotiva, este trabalho busca correlacionar os modelos disponíveis na
literatura com resultados de medições experimentais.
2
Dinâmica de frenagem do veículo
Durante o
processo de frenagem, há transferência de carga do eixo traseiro do veículo
para a dianteira. Essa variação nas cargas verticais, atuando nos pneus frontais
e traseiros, influencia na capacidade das forças de frenagem geradas entre pneu
e pista. Então, o modelo de frenagem utilizado deve considerar efeitos como a variação
de pressão entre os pneus ou a atuação do anti-lock braking system (ABS) [8].
A magnitude da
transferência de carga depende da desaceleração do veículo, da altura do centro
de gravidade (CG) e da distância entre eixos do mesmo. Assim, um automóvel com
entre eixo, relativamente, mais curto e CG mais alto sofre maior transferência
de carga para o eixo dianteiro do que um veículo longo e baixo.
No projeto do
sistema de freio veicular, a força de frenagem entre os eixos dianteiro e
traseiro são diferentes, por causa desta transferência de carga. Assim, para
avaliar a capacidade de frenagem, a partir dos dados do veículo e considerando
o atrito entre pneu e pista  , o coeficiente de resistência ao
rolamento
, o coeficiente de resistência ao
rolamento  e a altura do CG
e a altura do CG  , estima-se a máxima desaceleração
possível para o eixo dianteiro (
, estima-se a máxima desaceleração
possível para o eixo dianteiro ( ) e traseiro (
) e traseiro ( ), conforme as equações (1) e (2) [9].
), conforme as equações (1) e (2) [9].
Sendo,  a aceleração da gravidade,
a aceleração da gravidade,  e
e  as distâncias entre as rodas esquerda
ao CG e roda direta ao CG,
as distâncias entre as rodas esquerda
ao CG e roda direta ao CG,  e
e  as distâncias dos eixos dianteiro ao
CG e traseiro ao CG e
as distâncias dos eixos dianteiro ao
CG e traseiro ao CG e  o entre-eixo do veículo. A razão
entre a força de frenagem no eixo dianteiro (
o entre-eixo do veículo. A razão
entre a força de frenagem no eixo dianteiro ( ) e total (
) e total ( ) é descrita pela variável
) é descrita pela variável 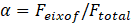 . Neste caso,
. Neste caso,  é variável entre 0 e 100% para
verificar a máxima capacidade de desaceleração do veículo.
é variável entre 0 e 100% para
verificar a máxima capacidade de desaceleração do veículo.
Portanto, a
capacidade de frenagem do veículo ( ), sem travamento de nenhuma das rodas
é dada pela menor aceleração entre as rodas, pois esta roda irá travar e
escorregar antes da roda com maior capacidade de desaceleração:
), sem travamento de nenhuma das rodas
é dada pela menor aceleração entre as rodas, pois esta roda irá travar e
escorregar antes da roda com maior capacidade de desaceleração:
3
Modelagem do sistema de freio
Neste
trabalho, a força de acionamento do freio é medida experimentalmente e
empregada na entrada do modelo matemático. Por hipótese, nos cálculos a seguir,
considera-se que não há travamento das rodas ou acionamento do ABS durante a
frenagem.
A força
aplicada no pedal de freio, pelo motorista, é multiplicada pela relação de
alavanca do pedal e somada à força auxiliar do hidrovácuo. Segundo Limpert, o
servo freio deve ser sensível o suficiente para que o motorista possa controlar
a efetividade do freio mesmo em baixas forças de atuação do pedal [10]. Assim, forças exercidas no pedal entre
13 a 22N devem iniciar a assistência de frenagem a vácuo. Para a estimativa da
força na saída do hidrovácuo ( ) foi empregado a formulação de Ho [11]:
) foi empregado a formulação de Ho [11]:
|
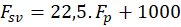
|
(4)
|
Sendo  a força no pedal de freio.
a força no pedal de freio.
A partir dessa
força, e o cilindro mestre formado por duas câmaras iguais, determina-se a
pressão da linha hidráulica ( ):
):
|
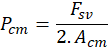
|
(5)
|
Sendo  a área da câmara do cilindro mestre.
a área da câmara do cilindro mestre.
Por
simplificação, desconsiderando as perdas de carga que ocorrem na tubulação de
freio, então, a força atuando no caliper é:
|
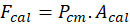
|
(6)
|
Sendo  a área do pistão no caliper.
a área do pistão no caliper.
Como a pinça
presente no veículo estudado é do tipo flutuante, a força de fechamento da
pinça ( ) é dada por:
) é dada por:
As pastilhas
de freio entram em contato com o disco, gerando uma força de atrito, que irá
fornecer o torque para a parada do veículo. Essa força de atrito  pode ser calculada pela equação a
seguir.
pode ser calculada pela equação a
seguir.
|
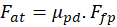
|
(8)
|
Sendo  o coeficiente de atrito entre a
pastilha e o disco.
o coeficiente de atrito entre a
pastilha e o disco.
Assim, o
torque de frenagem ( ) é definido como:
) é definido como:
|

|
(9)
|
Cujo,  é o raio efetivo do disco, ou seja, o
ponto médio da aplicação da força de atrito entre a pastilha e o disco.
é o raio efetivo do disco, ou seja, o
ponto médio da aplicação da força de atrito entre a pastilha e o disco.
Para
determinar a força de frenagem  atuando na roda, é preciso dividir o
torque de frenagem gerado no contato entre a pastilha de freio e o disco pelo
raio da roda.
atuando na roda, é preciso dividir o
torque de frenagem gerado no contato entre a pastilha de freio e o disco pelo
raio da roda.
Sendo  o raio dinâmico da roda.
o raio dinâmico da roda.
Analogamente,
para o tambor de freio nas rodas traseiras, a força de atrito ( ) é dada por
) é dada por
|

|
(11)
|
Sendo  o atrito gerado entre a sapata e a
parte interna do tambor e
o atrito gerado entre a sapata e a
parte interna do tambor e  a força de fechamento da sapata,
calculada da mesma forma que
a força de fechamento da sapata,
calculada da mesma forma que  (eq. (7)).
(eq. (7)).
Então, o
torque de frenagem ( ) nas rodas instaladas com um sistema
de tambor é:
) nas rodas instaladas com um sistema
de tambor é:
|

|
(12)
|
Sendo  o raio do tambor.
o raio do tambor.
A força de
frenagem nas rodas com o tambor será,
Como a força
de frenagem é a mesma nas rodas de cada eixo, é possível determinar a força
máxima, por eixo, como o dobro da força em cada roda. Assim, a força de
frenagem total é a soma dos dois eixos. A desaceleração resultante das forças,
em função da massa do veículo  , é:
, é:
Como
eficiência do sistema de freio, segundo Limpert [10], o sistema hidráulico tem 96% para freio a tambor e 98% para
freio a disco, e o pedal de freio tem eficiência de 80%, incluindo a eficiência
do cilindro mestre e molas de retorno.
4
Teste de frenagem
Segundo
Kumbhar, Patil e Sawant, o teste de frenagem é um procedimento para checagem
periódica de que os freios de um veículo estão funcionando em um nível que não
coloque as pessoas em perigo [12].
Os principais parâmetros
usados para definir o desempenho de um sistema de freios são:
• Tempo
de parada: O tempo decorrido entre o momento que a força de frenagem é aplicada
ao pedal e o momento que o veículo para (considerando parada completa);
• Distância
de parada: A distância percorrida pelo veículo desde o momento que o motorista
começa a atuar no pedal de freio até o momento de parada completa [12].
Segundo a ABNT,
existem diferentes tipos de testes, específicos para cada categoria de veículos
[13]:
• Tipo 0:
ensaio de desempenho ordinário com freios frios;
• Tipo I:
Ensaio de perda de eficiência por temperatura;
• Tipo
II: Ensaio de comportamento em declive;
• Tipo II
A: Ensaio de desempenho de frenagem de resistência;
• Tipo
III: Ensaio de fade para veículos de categoria O4.
Os testes
realizados neste trabalho são para veículos da categoria M1 (veículo projetado
e construído para o transporte de passageiros, que não tenham mais que oito
assentos, além do assento do motorista), voltado aos ensaios do Tipo 0, como
dados para validação do modelo matemático.
5
Metodologia
O veículo
empregado no teste é um Renault Sandero Expression 1.6L, modelo 2015, motor
Flex (Figura 1). Os dados do sistema de freio e veículo são
apresentados na Tabela 1 obtidos do manual do veículo e catálogos de fabricantes
[14].

Figura 1: Veículo testado no ensaio tipo O.
Tabela 1: Dados do veículo.
|
Parâmetro
|
Variável
|
Valor
|
|
Entre eixo
|

|
2,589m
|
|
Massa
|

|
1223,00kg
|
|
Relação pedal
|
-
|
3,125
|
|
Raio do cilindro mestre
|
-
|
10,32mm
|
|
Área do cilindro mestre
|

|
334,59mm²
|
|
Raio do hidrovácuo
|
-
|
115,00mm
|
|
Pressão do hidrovácuo
|
-
|
304,00mmHg
|
|
Raio pistão cáliper
|
-
|
24,00mm
|
|
Área do pistão do cáliper
|

|
1.809,56mm²
|
|
Raio disco freio
|

|
129,00mm
|
|
Raio cilindro de
roda
|
-
|
9,53 mm
|
|
Raio tambor
|

|
101,75 mm
|
|
Pneu
|
-
|
185/65 R15
|
Para a
aquisição dos dados durante os testes no veículo, foi utilizado sistema de
aquisição de dados (plataforma Arduino) com taxa de amostragem de 10Hz, cujo
circuito é ilustrado na Figura 2, associado a célula de carga (duas de 50kgf máximo
cada), instalada no pedal de freio, e acelerômetro inercial de 3 eixos (range
de ±2g), instalado no painel do veículo (Figura 3). Também, foram adquiridos os sinais da instrumentação
comercial do veículo através da porta OBD2. Este último é empregado para a
leitura da velocidade instantânea do veículo.
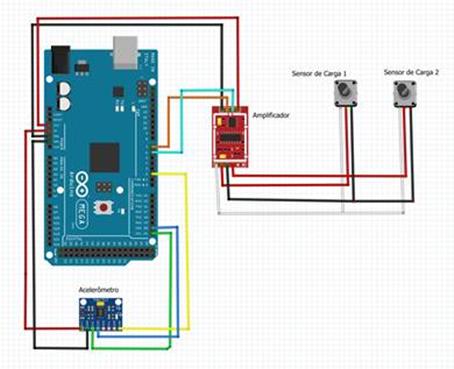
Figura 2: Ilustração da instrumentação no
veículo.

Figura 3: Posição do acelerômetro inercial no
painel.
A sequência de
testes realizados, para a validação do modelo matemático, foi realizada em duas
condições:
• Condição
1: acionamento forçado no pedal, de 60 km/h até a parada total;
• Condição
2: frenagem suave de 50 km/h até a parada total.
Como a
desaceleração muda de acordo com a força no pedal de freio, é necessário
analisar no modelo matemático os valores instantâneos da aceleração em função
da variação na força no pedal, obtido diretamente pela equação (14). O valor da desaceleração é, então, integrado numericamente
no tempo a fim de obter a curva de velocidade e compará-la com a velocidade
real do veículo obtida pelo OBD2.
A análise da
dinâmica do veículo na frenagem é, também, avaliada com imagens de vídeo
captada de uma câmera externa, para processamento e cálculo da distância e
tempo de frenagem via software Tracker [15] como ilustrado na Figura 4.

Figura 4: Gravação em vídeo para processamento
de imagem no software Tracker [15].
6
Resultados
A seguir são
apresentados os resultados comparativos entre o modelo matemático e medição
determinando a desaceleração instantânea, em função da força medida no pedal de
freio, e valores globais de distância percorrida e tempo gasto na frenagem.
Este último parâmetro não considera o tempo de reação do usuário, que de acordo
com Long, Gillespie e Tanaka varia pela reação cognitiva de até 74% do tempo pela
atenção ao trânsito, conversa em celular ou mensagem etc [16].
6.1
Limite de travamento das rodas
Utilizando o
modelo dinâmico do veículo, equação (1) a (3), para os valores da Tabela 2 como aproximação da condição do teste, determina-se a
curva de máxima desaceleração permitida, antes do travamento das rodas, e
escrita em função da razão da força de frenagem ( ). A curva é apresentada na Figura 5.
). A curva é apresentada na Figura 5.
Tabela 2: Dados da pista e condição do veículo.
|
Parâmetro
|
Valor
|
|
Coeficiente de atrito entre pneu e pista ( ) )
|
0,80
|
|
Coeficiente de resitência ao rolamento ( ) )
|
0,027
|
|
Altura do CG ( ) )
|
70 cm
|
|
Distância entre rodas do eixo ao CG ( e e  ) )
|
0,76 m
|
|
Distância do eixo frontal ao CG ( ) )
|
1,02 m
|
|
Distância do eixo traseiro ao CG ( ) )
|
1,57 m
|
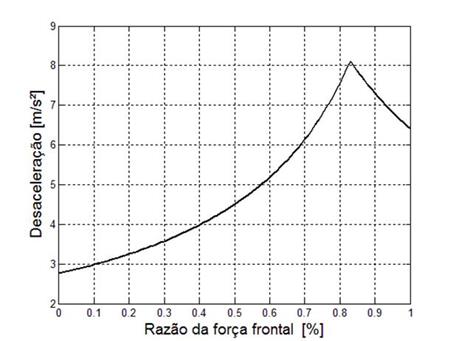
Figura 5: Máxima desaceleração ( ) em função da razão de força de
frenagem (
) em função da razão de força de
frenagem ( ).
).
Nesta a maior
taxa de frenagem possível, indicado pelo pico do gráfico, é de 8,1 m/s² quando 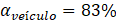 . Ou seja, do total de força exercida
através do sistema de freio, 83% deve ser no eixo dianteiro e 17% no eixo
traseiro.
. Ou seja, do total de força exercida
através do sistema de freio, 83% deve ser no eixo dianteiro e 17% no eixo
traseiro.
Comparativamente,
pelo sistema de acionamento do freio, as forças do eixo dianteiro e traseiro
podem ser obtidas diretamente através das relações mecânicas e hidráulicas do
veículo de teste, pelas equações (10) e (13), respectivamente, para o disco e tambor de freio. Determinando,
assim, a razão de força:
|
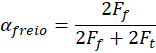
|
(15)
|
A partir dos
dados da Tabela 1, chega-se em 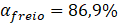 . Portanto, o modelo dinâmico, do
tópico 2, aproxima-se relativamente bem da proporção projetada ao veículo real de
83% obtido da Figura 5 (diferença de 4,5%). Assim, considerando que o modelo
representa a dinâmica do veículo, pela Figura 5, não haverá travamento das rodas se a desaceleração do
teste for inferior à 8m/s².
. Portanto, o modelo dinâmico, do
tópico 2, aproxima-se relativamente bem da proporção projetada ao veículo real de
83% obtido da Figura 5 (diferença de 4,5%). Assim, considerando que o modelo
representa a dinâmica do veículo, pela Figura 5, não haverá travamento das rodas se a desaceleração do
teste for inferior à 8m/s².
Portanto, as
diferentes condições do ensaio foram realizadas para que o valor medido da
desaceleração não ultrapassasse esse limite. Como forma de garantir que não
haveria escorregamento do pneu durante a frenagem ou o acionamento do freio ABS.
6.2
Comparativo da dinâmica veicular (modelo x real)
Na análise
seguinte, apresentam-se duas condições de frenagem com duas medições realizadas
para cada uma, que resultaram em perfis similares de desaceleração.
Para a
condição 1, foi atingida uma velocidade de aproximadamente 60 km/h e então
efetuada uma frenagem forçada (Figura 6), onde o motorista pisa no pedal de freio com uma força
um pouco maior do que a normal para uma atuação no cotidiano.
As curvas no
tempo da velocidade do veículo obtida pelo OBD2, a força no pedal (célula de
carga) e desaceleração (acelerômetro) são apresentados na Figura 6.
Neste teste, o
veículo é acelerado do repouso até 60 km/h e, então, o acionamento do freio é
feito após 21 s, que chegou a um pico de 5,5 kgf e depois se mantendo em uma
faixa de 2,5 a 3,5 kgf até o final do percurso, quando a velocidade final é
zero. A desaceleração máxima, no início do acionamento, foi próxima a 4,0m/s².
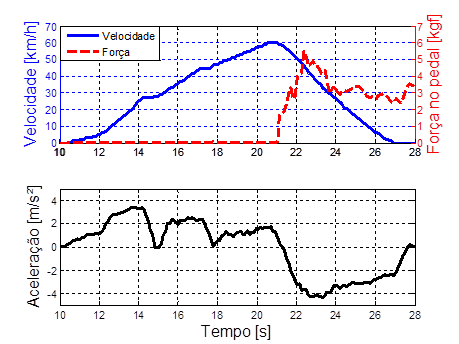
Figura 6: Condição 1: (a) velocidade do veículo
e força no pedal de freio e (b) aceleração do veículo.
É possível
perceber na Figura 7, que compara a curva de velocidade obtida pelo modelo
analítico e experimental, no início as curvas se mantêm similares, mas a partir
de 23,5 segundos, o resultado analítico começa a se distanciar do experimental.
Entretanto, de modo geral, a estimativa do desempenho veicular através da
modelagem apresentada anteriormente indica uma boa correlação com as avaliadas
experimentalmente. Uma das razões para o modelo analítico não ter resultado em
uma curva similar à curva experimental se deve ao fato de que a análise do
sistema do servo freio foi feita a partir da força de atuação do motorista
sobre o pedal, o que não é uma aproximação precisa, pois o servo atua também de
acordo com curso do pedal.
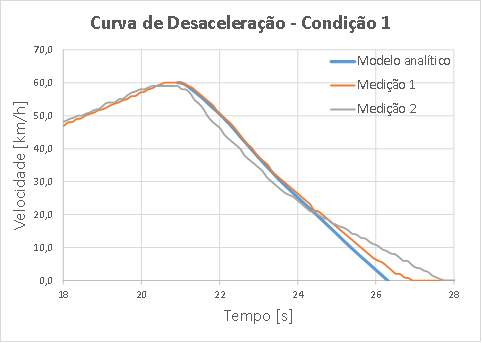
Figura 7: Condição 1: Comparativo da velocidade
entre modelo matemático e experimental.
Através da
integração numérica (método trapezoidal) da curva no tempo da velocidade, determinam-se
a distância e tempo de frenagem totais, conforme comparado na Tabela 3. A diferença percentual, respectivamente, é
aproximadamente de 6% e 8% entre o modelo e o experimental, indicando uma
relativa precisão do modelo matemático para prever o comportamento dinâmico do
veículo.
Tabela 3: Resultados de distância e tempo de
frenagem na condição 1.
|
Parâmetro
|
Distância
|
Tempo
|
|
Medido
|
48 m
|
5,8 s
|
|
Modelo
|
45 m
|
5,3 s
|
|
Erro
|
6,25%
|
8,62%
|
Na segunda
condição de frenagem iniciada aos 17 s (a partir de 50 km/h), Figura 8, a força aplicada atingiu 2,5 kgf e se manteve entre
esse valor e 1,5 kgf durante todo o ensaio. Isso resultou na curva de
desaceleração quase constante, atingindo aproximadamente 1,9 m/s². A metade da
desaceleração em relação à condição 1.
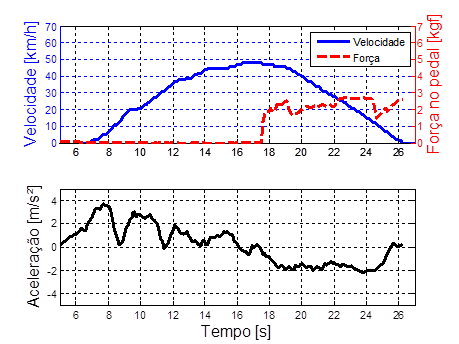
Figura 8: Condição 2: (a) velocidade do veículo
e força no pedal de freio e (b) aceleração do veículo.
Avaliando as
curvas de velocidade entre o modelo e pelo OBD2 na Figura 9, a tendência de desaceleração nas linhas é próxima das
duas medições realizadas. Entretanto, similar à condição 1, há uma diferença
nas curvas, o que é explicitado nos valores absolutos da distância percorrida e
tempo total de frenagem (Tabela 4), respectivamente, de 11% e 10%. Contudo, pelas
simplificações empregadas na modelagem, os resultados ainda são relativamente
precisos para uma estimativa do desempenho dinâmico do veículo.
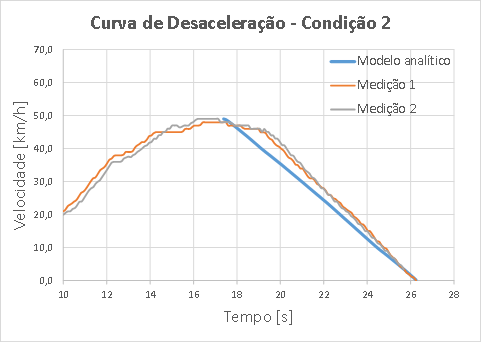
Figura 9: Condição 2: Comparativo da velocidade
entre modelo matemático e experimental.
Tabela 4: Resultados de distância e tempo de
frenagem na condição 2.
|
Parâmetro
|
Distância
|
Tempo
|
|
Medido
|
54 m
|
8,1 s
|
|
Modelo
|
60 m
|
8,9 s
|
|
Erro
|
11,1%
|
9,9%
|
A correlação
na inclinação das curvas de desaceleração é avaliada através de Análise de
Covariância (ANCOVA) [17], normalmente empregada em conjunto
com a regressão linear. As inclinações obtidas são verificadas se são paralelas
e estatisticamente sem diferença significativa. A hipótese nula ( ) é para inclinações iguais entre as
curvas (modelada e experimentais). O resultado é apresentado na Tabela 5. Pelo P-Value, acima de
) é para inclinações iguais entre as
curvas (modelada e experimentais). O resultado é apresentado na Tabela 5. Pelo P-Value, acima de  , conclui-se que as inclinações entre
as curvas medidas e modelada, para as duas condições, não apresentam diferenças
significativas.
, conclui-se que as inclinações entre
as curvas medidas e modelada, para as duas condições, não apresentam diferenças
significativas.
Tabela 5: Análise por ANCOVA da inclinação da
velocidade no tempo (desaceleração).
|
Condição
|
01
|
02
|
|
Inclinação modelo
|
-12,88
|
-5,44
|
|
Inclinação teste 1
|
-10,36
|
-6,23
|
|
Inclinação teste 2
|
-11,55
|
-6,96
|
|
P-Value
|
0,7437
|
0,7785
|
7
Conclusões
Com o grande
número de veículos dentro do mercado nacional, é de grande importância realizar
testes e cálculos dos componentes de segurança com rapidez e confiabilidade. Assim,
modelos matemáticos para predição do funcionamento desses sistemas são uma
ótima solução para o projeto das engenharias. Em particular, o sistema de freio
é um elemento sensível à segurança veicular e requer muitos ensaios antes da
homologação do produto veicular. Neste trabalho, modela-se matematicamente o
sistema de acionamento do freio para prever a capacidade de desaceleração do
veículo. Os resultados desses cálculos são comparados com dados medidos
experimentalmente, como forma de validação da metodologia empregada no modelo.
O modelo matemático
tem resultados da resposta de velocidade em função do tempo próximos aos
experimentais. Testado em duas situações, na condição 1 (frenagem forçada), a
diferença na distância de parada ficou em 6,25% e do tempo de parada em 8,62 s.
Já para a condição 2, os valores de distância e tempo foram de 11,1% e 9,9%,
respectivamente. Assim, indicando uma razoável representatividade do modelo ao
veículo real. Também, observado pelo paralelismo entre as inclinações das
curvas modelada e experimentais avaliado estatisticamente pela ANCOVA.
O modelo
resultante representa o veículo apresentado no trabalho, mas necessita de
ajustes dos parâmetros para outros veículos, com diferentes configurações, ou
na mudança geométrica dos componentes do sistema de freio.
Portanto, como
uma forma de modelagem simplificada para estimar o desempenho em diferentes
condições de uso do sistema de freio, o procedimento se mostra adequado. Tal
como para avaliar impactos na variação de seus parâmetros na eficiência do
sistema, por exemplo, em um estudo da sensibilidade das variáveis de projeto no
desempenho veicular em frenagem. Este tipo de abordagem pôde auxiliar as
engenharias no desenvolvimento e otimização desse sistema crítico do produto [18].
Referências
[1] HAPPIAN-SMITH, J.
Introduction to modern vehicle design. In: CROLLA, D. A.; Automotive
engineering: powertrain, chassis system and vehicle body. Oxford: Elsevier,
2004.
[2] GENTA, G.; MORELLO, L., CAVALLINO, F.
et al. The
motor car: past, present and future. Dordrecht: Springer Science, 2014.
[3] ISHAK, M.R.; BAKAR, A.R.A.;
BELHOCINE, A; TAIB, J.M.; OMAR, W.Z.W. Brake torque analysis of fully
mechanical parking brake system: Theoretical and experimental approach. Measurement,
n. 94. páginas 487-497, 2016.
[4] GILLESPIE, T. D.
Fundamentals of vehicle dynamics. Warrendale: Society of Automotive Engineers,
Inc., 1992.
[5] XIA R.; WU, D.; HE, J.;
LIU, Y.; SHI, D. A New Model of Stopping Sight Distance of Curve Braking Based
on Vehicle Dynamics. Discrete Dynamics in Nature and Society, 2016.
[6] YANG, S.; LU, Y.; LI, S.
An overview on vehicle dynamics. International Journal of Dynamics and Control,
n. 1. páginas 385-395, 2013. (doi.org/10.1007/s40435-013-0032-y)
[7] AHMAD, F.; MAZLAN, S.A.;
ZAMZURI, H.; JAMALUDDIN, H.; HUDHA, K.; Short, M. Modelling and validation of
the vehicle longitudinal model. International Journal of Automotive and
Mechanical Engineering, n. 10. páginas 2042-2056, 2014.
[8] BLUNDELL, M.; HARTY, D.
The Multibody Systems Approach to Vehicle Dynamics. In: CROLLA, D. A.;
Automotive engineering: powertrain, chassis system and vehicle body. Oxford.
Elsevier, 2004.
[9] WONG, J. Y. Theory of
Ground Vehicles. New York: John Wiley & Sons, 2001
[10] LIMPERT, R. Brake design
and safety. Warrendale: SAE International, 1999.
[11] HO, H. P. The influence of
braking system component design parameters on pedal force and displacement
characteristcs. PhD Thesis. Badford University, UK, 2009.
[12] KUMBHAR, B. K.; PATIL, S.
R.; SAWANT, S. M. A Comparative study on automotive brake testing standards.
Journal of the Institute of Engineers, Maharashtra (India), Series C, 2017.
[13] ASSOCIAÇÃO BRASILEIRA DE NORMAS
TÉCNICAS. NBR 10966-2. Veículos rodoviários automotores — Sistema de freio
Parte 2: Ensaios de frenagem e desempenho para veículos das categorias M, N e
O. Rio de Janeiro: ABNT, 2015.
[14] RENAULT. Renault SANDERO: Manual do
proprietário, 2015.
[15] BROWN, D. Tracker Video
Analysis and Modeling Tool for Physics Education. Disponível em:
<https://physlets.org/tracker/>. Acesso em: 20 mar. 2020.
[16] LONG, B.L.; GILLESPIE, A.I.;
TANAKA, M.L. Mathematical Model to Predict Drivers’ Reaction Speeds. Journal of
Applied Biomechanics, n. 28. páginas 48-56, 2012.
[17] SELTMAN, H.J. Experimental
Design and Analysis. Carnegie
Mellon University, 2012. Disponível em: <https://www.e-booksdirectory.com/details.php?ebook=8161/>.
Acesso em: 19
nov. 2020.
[18] BREUER, B. Brake
Technology Handbook. SAE International; 1st edition, 2008.
orcid.org/0000-0002-6818-5086
orcid.org/0000-0002-3853-0758
![]()
![]()