1
Introdução
A energia é um
insumo basilar nas economias modernas. A história do desenvolvimento econômico
e social de todos os países está intimamente relacionado ao desenvolvimento e a
expansão da oferta de energia elétrica. De acordo com a Empresa de Pesquisa
Energética - EPE, a matriz elétrica do Brasil é baseada principalmente em
fontes renováveis, sendo a hidráulica a principal fonte de geração de energia
elétrica (65,2%), seguida por gás natural (10,5%), Biomassa (8,2%), energia Solar
e Eólica (6,9%), Carvão (4,1%), energia Nuclear (2,6%) e Petróleo e Derivados
(2,5%) [1].
A geração de
energia elétrica ocorre em ambiente de livre concorrência com a venda da
energia por meio de leilões ou de livre negociação. Geralmente os contratos de
compra e venda de energia são de longo prazo, o que minimiza o risco inerente
do setor.
O principal
sistema de transmissão nacional é todo integrado (conhecido como SIN – Sistema
Integrado Nacional) e visa ligar as diversas regiões do país através de
subsistemas: Sul, Sudeste-Centro-Oeste, Nordeste e Norte.
Especificamente
sobre Subsistema Nordeste, a energia elétrica que era produzida provinha
basicamente da fonte hídrica - com grande importância das águas do Rio São
Francisco. Em tempos mais recentes, este cenário vem se modificando com a
abertura para outras fontes de geração de energia elétrica. Destaca-se o
crescimento expressivo e do aumento da capacidade instalada da geração eólica,
muito por reflexo de ser uma via alternativa as baixas precipitações pluviométricas
que a região vivencia e pela quantidade de dias ensolarados que a região
experimenta. Dados, na posição de fevereiro/2019, revelam que a fonte eólica já
lidera a matriz de energia elétrica do Nordeste com participação de 35,46%,
seguida da fonte hidráulica, com 32,49% [2].
Apesar do
crescimento expressivo da fonte eólica, o Subsistema Nordeste ainda se mostra
deficitário, sendo importador líquido de energia elétrica. Em 2018 este déficit
de geração de energia elétrica chegou a 1.642 MW médios, o que equivalia a
15,2% da carga [2]. Assim, faz-se
necessário investigar como essas mudanças afetam a demanda por energia elétrica
na região Nordeste.
Essa pesquisa
deriva do fato da energia elétrica não possuir uma viabilidade técnico-econômico
de ser armazenada, sua produção e consumo devem ser cuidadosamente planejados
de forma a evitar situações de insuficiência energética (falta de
abastecimento), bem como de superprodução (desperdício). Desta forma, possuir
uma ferramenta de previsão de demanda de energia é fundamental para auxiliar o
processo de tomada de decisão e de investimentos por parte dos entes
envolvidos.
2
Materiais
e métodos
Nesta seção é
apresentada os conjuntos de dados selecionados para o estudo, a metodologia
para desempenhar a previsão de séries temporais usando modelos clássicos e de machine
learning, e os detalhes do estudo experimental desempenhado.
2.1
O
Operador Nacional do Sistema Elétrico (ONS)
Após a
definição do problema de negócio: “Previsão do consumo de energia elétrica na região
Nordeste do Brasil” sendo modelado como um problema de previsão univariado um
passo à frente deve-se identificar o Stakeholder que contém a serie a ser
usada, neste caso o ONS.
O ONS contém
diversas informações energia no território brasileiro. Para este trabalho foi
usada a variável Carga de Energia (CE). Ela contém registros diários do consumo
de energia da região Nordeste do Brasil no período compreendido entre 2004 a
2019, totalizando 5.844 observações.
2.2
Análise
descritiva dos dados do ONS
A primeira
análise que pode ser feita à variável CE é uma estatística. As 5.840
observações dão uma ideia de quantas observações podem ser usadas para
treinamento e teste para um modelo de machine learning. A média de 8.559
aproximadamente seria linha base da série temporal. O desvio padrão dá uma
ideia da distância dos valores em relação à média. Neste caso tem-se um alto
desvio dos dados. Têm-se os percentis para elaborar o boxplot. Os valores
máximo e mínimo que podem ser usados para normalizar a série temporal.
count
5840.000000
mean
8558.735315
std
1500.038727
min
5193.175417
25%
7279.704927
50%
8507.408812
75%
9858.647688
max
13536.630628
Pode-se elaborar
um gráfico de linhas (Figura 1) para observar rapidamente algumas
características como possíveis valores anómalos, componentes de tendência e
sazonalidade. Assim, é possível observar claramente que existe uma tendência.
Também é possível observar a presença de um provável outlier entre os
anos 2014 – 2016. Também pode-se observar uma componente sazonal anual.
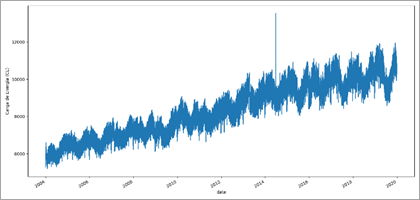
Figura 1. Gráfico de linhas
para a variável CE.
Esta primeira
análise é importante porque guiará a seleção do modelo linear (Ex. Modelo SARIMA).
Também ditas componentes podem ser usados como séries de entrada para os
modelos de machine learning (Ex. LSTM). E os possíveis outliers
podem ser processados com alguma técnica de seleção de características (Ex. Random
Forest). Esta fase de pré-processamento de dados também pode ser chamado de
Engenharia de Características.
Uma outra
visualização importante é a distribuição dos dados, o gráfico de densidade
(Figura 2) é elaborado a partir do Histograma. Este é um gráfico sem ordem
temporal. Trata-se de um gráfico importante já que alguns métodos de previsão
de séries temporais lineares, como os modelos SARIMA, assumem uma distribuição
de observações do tipo Normal ou Gaussiana. Na Figura 2 pode-se observar que
certamente existem duas gaussianas superpostas ou uma Gaussiana Dupla.
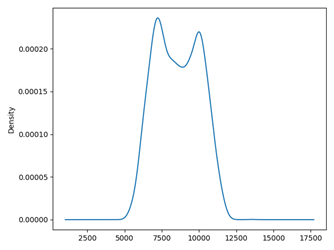
Figura 2. Gráfico de densidade
para a variável CE.
Uma maneira de
analisar a distribuição dos dados por intervalo é usar o gráfico de boxplot
(Figura 3). Este tipo de gráfico utiliza os percentis calculados anteriormente
para desenhar as caixas por ano. A linhas centrais das caixas representa a
mediana desse conjunto anual de dados. É importante notar que os pontos fora
das caixas são chamados de pontos exteriores (valores atípicos). Uma forma de
processar esses dados é extrair os valores atípicos. Ou seja, entregar para o
modelo sem esses valores atípicos e avaliar o desempenho do modelo.
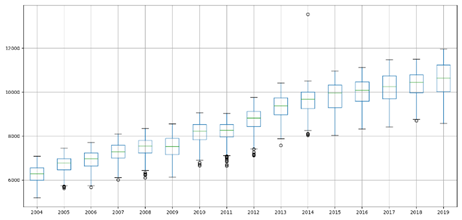
Figura 3. Gráfico Boxplot para
a variável CE.
A modelagem de
séries temporais assume uma relação entre uma observação e sua observação
passada. Essas observações passadas são chamadas de lag. Podem-se criar
gráficos de uma variável com seus lags (lag-1, lag-2, etc.) como
mostrado na Figura 4. Analisando os gráficos para a variável CE e seus lags,
pode-se inferir que existem uma correlação positiva. Em outras palavras, existe
uma relação linear entre CE e seus valores passado até lag-7. Este tipo de
gráfico poderia ser usado para determinar a ordem ‘p’ de um modelo SARIMA, ou
seja, p=7 (de tendência).
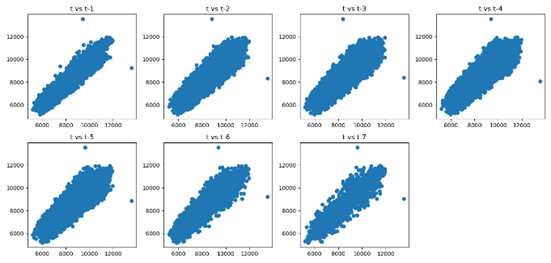
Figura 4. Gráfico de dispersão
contendo lag-7 para a variável CE.
Existe outro
tipo de gráfico chamado de autocorrelação que pode mensurar a relação linear de
uma variável com seus lags. Este valor varia entre -1 e 1, significando que
o valor 1 representa uma forte correlação positiva e que o valor -1 uma forte
correlação negativa. Já o valor 0, representa a ausência de correlação. Na
Figura 5, pode-se observar os graus de correlações lineares entre a variável CE
e seus 6.000 primeiros lags, sugerindo que poderiam ser usados os
primeiros 400 lags, aproximadamente. Este gráfico pode ser usado para
selecionar quantos lags de cada variável podem ser selecionados tanto para
modelos lineares como de machine learning.
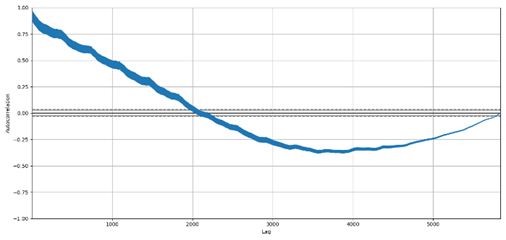
Figura 5. Gráfico de
autocorrelação para a variável CE.
2.3
Metodologia
Nesta subseção
são descritos os principais passos de pré-processamento e os conceitos
fundamentais por trás dos modelos persistente, clássicos (ARIMA, SARIMA) e de
redes neurais (MLP, CNN, LSTM) utilizadas.
2
2.1
2.2
2.3
2.3.1
Pré-processamento
dos dados
Uma vez feito
o download das tabelas temporais associadas ao problema de pesquisa, cada tabela contendo um
conjunto de atributos, é necessário fazer o pré-processamento visando a
adequação dos dados para serem as entradas dos modelos de previsão de séries
temporais.
Lembrando que
nesta fase se objetiva montar a tabela de treinamento e de teste para que o
modelo clássico e de machine learning possam desempenhar a previsão da
variável em estudo.
Cabe mencionar
que todas as colunas que não foram usadas pelo modelo foram excluídas usando o
Excel (Figura 6), resultando em tabelas basicamente com colunas temporal e de
atributo (Figura 7). Por outro lado, o tratamento da coluna temporal foi
formatado para o formato (YYYY-MM-DD), usando o Excel.
Figura 6. Colunas com
atributos contendo valores repetitivos associadas à tabela CE.
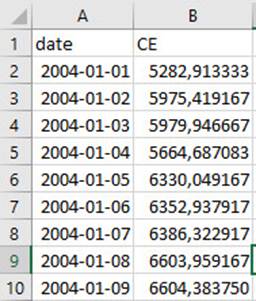
Figura 7. Formato final da tabela CE.
Um outro
aspecto de transformação de dados diz respeito à normalização entre 0.10 e
0.90. Neste quesito foi adotado a transformação linear seguindo a equação (1) e
a Tabela 1:
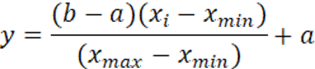 (1)
(1)
Onde Xmin
e Xmax são os valores mínimo e máximo da série temporal associada à
variável em questão.
Tabela 1. Valores adotados para normalização.
No caso da
variável CE, os seus valores antes e despois da normalização ficaram como
mostrado na Figura 8.
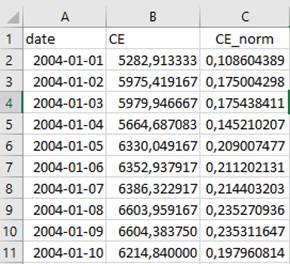
Figura 8. Variável CE antes e
despois da normalização.
2.3.2
Modelos
Naive
Estas
abordagens apenas proporcionam o baseline de desempenho (limiar
inferior) associado ao problema. Desta forma, pode-se obter uma ideia de quão
bom os demais modelos (mais sofisticados) se desempenham nesse problema [3]. Embora simples, eles podem ser
ajustados a um determinado problema. Por exemplo, no modelo persistente definir
a observação na qual vai persistir. Para a estratégia baseada em média ou
mediada deve-se definir quantas observações passadas devem ser escolhidas. A
sintonização destes hiperparâmetros podem prover um limite inferior mais
robusto sobre o desempenho do modelo. Além disso, podem ajudar na escolha e
configuração de métodos mais sofisticados.
Estratégia
Persistente
Usa uma das
observações passadas como valor de previsão. Pode ser ajustado para observações
sazonais. Neste caso, a observação no mesmo tempo do ciclo (offset)
anterior talvez seja usado. Pode-se generalizar para testar diferentes offsets.
Não se faz tratamento nos dados.
Estratégia
baseada em Média ou Mediana
Calcula a
média ou mediana de um conjunto de observações prévias para logo ser usada como
valor de previsão sem
nenhum tratamento nos dados. O conjunto de observações pode ser fixado a um
número reduzidos das últimas observações passadas ou generalizado para testar
cada possível ‘n’ conjuntos de observações passadas para calcular a média ou
mediana.
2.3.3 Modelos Autoregressivos
ARIMA/SARIMA
O modelo ARIMA
(AutoRegressive Integrated Moving Average) é uma classe de método
estatístico para analisar
e fazer previsão de séries temporais. É uma
generalização de um modelo mais simples chamado ARMA (AutoRegressive Moving
Average), na qual é adicionada a noção de integração [3][4]. Os aspectos chaves do modelo podem
ser descritos como segue [5]:
• AR: Autoregressão. Um modelo que usa a relação
dependente entre uma observação e um número de observações defasadas;
• I: Integrado.
O uso de diferenciação nas observações (subtraindo cada observação com sua
observação prévia imediata) com o objetivo de tornar série temporal
estacionária;
• MA:
Médias Móveis. Um modelo que usa a dependência entre uma observação e um
erro residual (calculado
quando aplicado um modelo de médias móveis a observações defasadas).
Pode
ser especificado como ARIMA (p, d, q), onde os parâmetros p (minúsculo, para a
ordem autoregressiva tendencial), d (minúsculo, para a ordem de diferenciação
tendencial) e q (minúsculo, para a ordem de médias móveis tendencial). Os
parâmetros devem ser números inteiros e configuram o modelo. As componentes AR,
I e MA, estão associadas aos parâmetros p, d, q respectivamente. O modelo ARIMA
não dá suporte a dados sazonais (séries temporais com período repetitivo). O
modelo ARIMA espera dados não sazonais ou dados cuja componente sazonal foi
removida usando diferenciação sazonal.
O
processo ARIMA implica construir um modelo de regressão linear considerando uma
ordem a cada parâmetro, e a séries temporal é tratada (por diferenciação) para
garantir sua estacionaridade, o qual se não for feita, pode afetar o desempenho
do modelo.
Por outro
lado, um modelo SARIMA (Seasonal AutoRegressive Integrated Moving Average)
é uma extensão do modelo ARIMA que suporta dados sazonais. Ele adiciona mais 4
parâmetros, P (maiúsculo, para a ordem autoregressiva sazonal), D (maiúsculo,
para a ordem de diferenciação sazonal), Q (maiúsculo, para a ordem de médias
móveis sazonal) e m (número de passos para um único período sazonal).
Configurar
tanto um modelo ARIMA quanto SARIMA implica atribuir valores aos parâmetros,
tanto na ordem sazonal quanto na tendencial. Para notação do modelo SARIMA
segue-se: SARIMA(p, d, q)(P, D, Q, t)m. Os gráficos ACF (AutoCorrelation
Function) e PACF (Partial AutoCorrelation Function) são usados para
definir de forma aproximada os parâmetros do ARIMA. Na prática um esquema de grid
search (teste de várias configurações de modelos SARIMA) é usado para
estimar os parâmetros.
2.3.4 Modelo MLP
Trata-se de
uma rede neural composta por camadas de neurônios que se ligam através de
sinapses com pesos. O MLP (MultiLayer Perceptron) é formado por 3 tipos
de camadas, uma de entrada, uma camada de saída e uma ou mais camadas ocultas (hidden
layers), onde ocorrem os cálculos computacionais [6]. Visto que o MLP é uma rede plenamente
conectada, os nós de cada camada se conectam imediatamente com os nós da camada
posterior e estas conexões são ponderadas pelos pesos. O MLP é muito utilizado
nos casos de problemas não lineares, onde um único hiperplano não consegue dar
bons resultados. A lógica de treinamento de um MLP é por algoritmo de
retropropagação de erro, que consiste em duas etapas: o processo direto e o
processo reverso. Inicialmente não se possui informações sobre os pesos da
rede, então, deve-se inicializar os pesos de forma aleatória com distribuição
uniforme próximo de zero. Assim, no processo direto a entrada de valor é
propagada pela rede e os pesos se mantém constantes. No processo reverso, um
sinal de erro da saída é propagado no sentido contrário ao sinal de entrada e
os pesos são corrigidos de acordo com algum regramento. Esse retroprocessamento
é contínuo e mantém-se até que critérios de parada sejam atendidos.
2.3.5
Modelo
CNN
Uma rede
neural convolucional é uma arquitetura de rede neural de aprendizado profundo e
que foi inspirada nos processos biológicos da visão. As conexões dos neurônios
se baseiam na forma como o córtex visual dos animais funciona. Por isso que
este tipo de rede é muito utilizado em problemas de reconhecimento de imagens.
Uma das vantagens de se utilizar uma CNN (Convolutional Neural Network)
é que o pré-processamento é menos custoso do que outros algoritmos de
classificação.
Nas CNNs
apenas subconjuntos de entradas são conectadas aos neurônios, o que é bem
diferente das redes ditas plenamente conectadas, onde todos os neurônios estão
conectados. Essa mudança de arquitetura faz com que se diminua o número de
parâmetros a serem aprendidos e, consequentemente, há um ganho de tempo no
processo de treinamento da rede [7].
2.3.6
Modelo
LSTM
Rede neural
desenhada para abordar problemas de sequência. Possui na sua arquitetura
conexões com loops, adicionando assim retroalimentação e memória. Esta
memória permite a rede aprender e generalizar através de sequências de entradas,
ao invés de padrões individuais. Um tipo de rede neural recorrente é a rede
LSTM (Long Short-Term Memory). A LSTM adquire potencial contrastado no
estado da arte quando concebidas de forma empilhada. Existe uma limitação para
o MLP para o caso de um problema de previsão de séries temporais univariado,
que quando se define a janela de entradas para o MLP esta é fixa e deve ser
escolhida com conhecimento baseado no contexto do problema. Em outras palavras,
um tamanho de janela inadequado não capturaria padrões relevantes para fazer
previsão univariado [8].
No que diz
respeito ao seu funcionamento e arquitetura, um neurônio pode passar seu sinal
para seus neurônios vizinhos além de passar o sinal para frente. A saída da
rede pode ser conectada à entrada da rede recorrente. As conexões recorrentes
adicionam um estado ou memória a rede, isto permite aprender uma maior extensão
de abstrações a partir da sequência de entradas. A diferença das MLPs que
possuem neurônios, as redes LSTMs possuem blocos de memória que são conectadas
em camadas. Esses blocos contêm comportas que gerenciam o estado do bloco e sua
saída. Uma unidade de memória opera sobre uma sequência de entrada e cada
comporta dentro de cada unidade usa uma função de ativação sigmoide para
controlar se eles são ativados ou não, fazendo uma mudança no seu estado e
adicionando informação para fluir através da unidade condicional. O algoritmo
de treinamento da RNN (Recurrent Neural Network) é chamado de Backpropagation
Through Time (BPTT). Cada unidade de memória é como um mini estado de máquina
onde as comportas da unidade possuem pesos que são aprendidos durante o treinamento.
Toda LSTM possui os seguintes componentes nas suas unidades de memória:
• Forget gate: Decide
que informação é descartada da unidade de memória;
• Input gate: Decide
quais valores da entrada devem ser usados para atualizar o estado da memória;
• Output gate: Decide
qual é a saída baseada na entrada e a memória da unidade.
No entanto, ainda existem os seguintes
desafios:
·
Como treinar uma
RNN com backpropagation;
·
Como lidar com os
temas de VANISHING e EXPLODING durante treinamento.
2.4 Estudo experimental
Nesta subseção
é apresentado o desenho do estudo experimental conduzido usando os dados associados
à variável em estudo. Além disso, são descritas as configurações dos modelos
para o processo de busca dos hiperparâmetros para cada arquitetura, a métrica
de avaliação e o teste de hipótese.
O conjunto de
dados do consumo de energia (Variável CE pertencente ao Stakeholder ONS) da
região Nordeste para previsão de um dia a frente. Ao todo têm-se 5.844
observações, das quais, 5.479 observações serão usadas como treinamento e o
restante, 365, como teste. Cabe dizer que para este cenário, serão apresentados
os 3 melhores modelos com menor erro associado.
Para rodar os
experimentos, usou-se um computador com processador Intel® Core™ i7, CPU 2.2Ghz
com 8.00GB RAM. Foi utilizada a linguagem Python 3.7 com o auxílio das
seguintes bibliotecas: TensorFlow 2.0, Keras, SKlearn, StatsModels e SciPy.
2.4.1
Modelos
A seguir são
expostos de maneira sucinta as principais configurações dos modelos
apresentados no item 2.3.2 até o 2.3.6 para desempenhar a busca dos
hiperparâmetros com o objetivo de testar vários modelos candidatos e escolher a
configuração que atingir um menor MAPE (Mean Absolute Percentual Error).
Modelo
Simples
Ao todo foram testadas
34.992 possíveis configurações baseadas em Persistente, Média e Mediana. Somado
a isso, testou-se modelos simples usando componentes sazonais de 12 meses, já que,
os dados usados de consumo apresentam um período sazonal de 12 meses ou 365
dias.
Modelo
SARIMA
Para fins de
simulação utilizou a seguinte configuração de SARIMA. A partir de um grid
search foram testados um total de 2.592 possíveis configurações. As
configurações dos parâmetros do modelo SARIMA foram: tendência (p, d, q = [ 0,
1, 2]) e sazonal (P, D, Q = [0, 1, 2]), com período sazonal m = 12 e sem
período sazonal m = 0 e quatro possíveis modelos de tendência [ ‘n’, ‘c’, ‘t’,
‘ct’], significando: n: sem tendência, c: constante, t: linear e ct: uma
constante com tendência linear.
Modelo
MLP
Para fins de
simulação se fixou uma rede neural de uma camada oculta com função de ativação
RELU, otimizador ADAM, função perda MSE (Mean Squared Error) e um
neurônio na camada de saída já que, trata-se de um problema de previsão um
passo à frente. Os hiperparâmetros que serão buscados no grid search
são: número de entradas igual a [12, 6, 24], número de neurônios na camada
oculta com possíveis valores de [25, 50, 75], número de épocas igual a [50,
100, 150], tamanho de minibatch com possíveis valores de [75, 100], a
ordem de diferenciação dos dados com possíveis valores de [0, 12]. Em conjunto
todas essas possibilidades fazem ao todo uma quantidade de configurações de
rede neural de 108, as quais foram repetidas 10 vezes cada por causa da
aleatoriedade dos pesos da rede neural. Em outras palavras, para cada configuração
de rede neural se executou 10 repetições e o valor final de desempenho foi a
média desses 10 valores MAPE.
Modelo
CNN
Para fins de
simulação se fixou uma rede neural convolucional de uma camada convolucional
com função de ativação RELU, função máximo para uma camada pooling, otimizador
ADAM, função perda MSE e um neurônio na camada de saída. Os hiperparâmetros que
serão buscados no grid search são: número de entradas igual a [12, 6,
24], número de filtros com possíveis valores de [32, 64], tamanho do kernel com
possíveis valores de [3, 5], número de épocas igual a [50, 100, 150], tamanho
de minibatch com possíveis valores de [75, 100], a ordem de diferenciação dos
dados com possíveis valores de [0, 12]. Em conjunto todas essas possibilidades
fazem ao todo uma quantidade de configurações de rede neural de 144 as quais
foram repetidas 10 vezes cada por causa da aleatoriedade dos pesos da rede
neural. Em outras palavras, para cada configuração de rede neural convolucional
foi executada em 10 repetições e se tomou como valor final de desempenho a
média desses 10 valores MAPE.
Modelo
LSTM
Para fins de
simulação se fixou uma rede neural LSTM de uma camada oculta com função de
ativação RELU, otimizador ADAM, função perda MSE e um neurônio na camada de
saída. Os hiperparâmetros que serão buscados no grid search são: número
de entradas igual a [12, 6, 24], número de neurônios na camada oculta com
possíveis valores de [25, 50, 75], número de épocas igual a [50, 100, 150],
tamanho de minibatch com possíveis valores de [75, 100], a ordem de
diferenciação dos dados com possíveis valores de [0, 12]. Em conjunto todas
essas possibilidades fazem ao todo uma quantidade de configurações de rede
neural de: 108, as quais foram repetidas 10 vezes cada por causa da
aleatoriedade dos pesos da rede neural. Em outras palavras, para cada
configuração de rede neural foi executado 10 repetições e se tomou como valor
final de desempenho a média desses 10 valores MAPE.
2.4.2
Métrica
de avaliação
Para avaliar o
desempenho de previsão univariado dos 5 tipos de modelos usados, foi usado o
Erro Percentual Médio Absoluto (MAPE). O MAPE pode ser definido com a equação
abaixo:
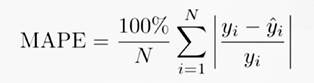 (2)
(2)
Onde: “N”
representa o número de exemplos para treinamento; yi representa o
valor atual (real) e yi (com chapéu) representa o valor da previsão
dado pelo modelo (clássico ou de aprendizado de máquina).
2.4.3
Teste
de hipótese
Para testar os
resultados das previsões dos modelos clássicos e de machine learning (dois
a dois), foi usado o método de teste de significância estatística de
Deibold-Mariano [9],
com modificação sugerida por Harvey [10] para estatisticamente comparar dois conjuntos de previsões. Adicionalmente,
utilizou-se um nível de significância do 5% (alpha = 0,05) para ser comparado
com o valor p (p-value), o qual é originado através do uso do teste [9] entre dois modelos de previsão e
discernir se a diferença associada ao desempenho MAPE entre dois modelos de
previsão é estatisticamente significativa ou não.
A continuação
é definida nas hipóteses Nula (Ho) e Alternativa (Ha). Cabe dizer que o teste
estatístico segue uma distribuição T-Student com grau de liberdade (T –
1), onde T é o cumprimento da série temporal.
·
Hipótese Nula
(Ho): Os algoritmos
provavelmente têm o mesmo desempenho.
·
Hipótese
Alternativa (Ha):
Provavelmente existe uma diferença real entre o desempenho médio dos algoritmos.
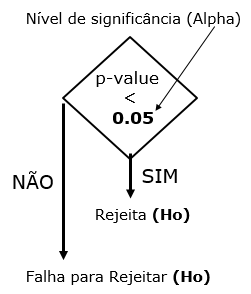
Figura 9. Verificação do p-value com o nível de significância (alpha)
para rejeição ou aceitação da H0.
3 Resultados e Discussões
Os resultados
com todas as previsões segundo as melhores configurações de cada modelo estão
apresentados na Tabela 2. De todas as possibilidades de configuração e
parâmetros que cada um dos modelos poderia adotar, foram escolhidos aquelas
configurações e parâmetros que retornaram o menor erro associado (MAPE).
Cabe lembrar
que a previsão diária do Nordeste que consta na Tabela 2, na realidade, é uma
média mensal das previsões diárias. Por exemplo, para o caso do modelo MLP
associado ao mês de janeiro tem-se o valor de 9788,26 MW, o qual expressa o
valor médio das 31 previsões médias diárias (lembrar que foram executadas 10
repetições por modelo por causa da estocasticidade dos modelos de machine
learning).
Para testar os
resultados das previsões dos modelos clássicos e dos modelos de machine
learning dois a dois foi utilizado o método de teste de significância
estatística de Deibold-Mariano [9], com modificação sugerida por Harvey [10] para que fosse possível comparar estatisticamente
dois conjuntos de previsões. Para tanto foi adotado a seguinte sequência de
comparação 2 a 2: (MLP v.s. CNN -> ganhador v.s. LSTM -> ganhador v.s. SARIMA
-> ganhador v.s. SIMPLES).
A escolha pelo
modelo mais eficiente se fez quando observado que: i) se no teste de hipótese
os modelos possuíam diferenças estatísticas, ou seja, a métrica do erro
associado aquele modelo comparado com o erro associado ao outro modelo foram
estatisticamente diferentes, optou-se pelo modelo de menor erro MAPE, visto que
os modelos não têm a mesma eficácia; ii) se o teste de hipótese dos erros
associados aos modelos não possuíssem diferença, estatisticamente significante,
ou seja, usar um ou o outro modelo traria a mesma qualidade de previsão,
optou-se por continuar escolhendo o modelo com menor MAPE associado.
Desta forma,
garantiu-se que o modelo escolhido era o robusto no trabalho de previsão ou por
diferença estatística do seu erro associado ou por possuir uma acurácia melhor
quando os modelos se mostraram equivalentes. A tabela 2 resume todos os
resultados e os valores p-value.
A Tabela 3 mostra
o modelo escolhido (coluna em destaque) baseado no teste de hipótese de
Deibold-Mariano. Cabe dizer que o caractere ‘x' significa que não foi
necessário comparar esses dois modelos associados já que segundo a sequência
adotada só o modelo vencedor é usado para ser validado com o modelo seguinte da
sequência.
4 Conclusões
Neste trabalho
foi proposto uma instigante metodologia de previsão de consumo de energia
elétrica utilizando dados temporais do consumo de energia e com auxílio diversas
arquiteturas de redes neurais obter a melhor configuração para previsão de um
passo temporal à frente.
Outrossim,
essa metodologia é facilmente replicada a outros conjuntos de dados ou
contextos, onde é possível prever a demanda de uma determinada região, por
exemplo: a demanda por energia elétrica de uma unidade federativa em particular
ou obter a demanda por um tipo específico de fonte geradora.
Previsões bem-sucedidas
orientam planejamentos que balizam investimentos. O setor elétrico é por
natureza complexo e intensivo em capital, ou seja, os valores dispendidos são
altos e o prazo de execução de novas obras são longos e custosos. Assim quanto
mais certeiras forem as previsões de oferta e demanda por energia elétrica, melhores
serão as decisões de investimento que beneficiarão as empresas, a população e o
próprio Sistema Integrado Nacional - SIN.
orcid.org/0000-0002-0631-8488
orcid.org/0000-0002-8212-4589