Os perfis
formados a frio são uma opção econômica na utilização de estruturas de aço, por
apresentarem menor consumo de material devido à baixa espessura das chapas que
os constituem, e devido aos processos de fabricação à temperatura ambiente
serem menos onerosos que aqueles dos perfis laminados e soldados. Além disto,
são versáteis e fáceis de transportar e movimentar no canteiro de obra [1].
No entanto,
por serem elementos esbeltos, as estruturas de aço em perfis formados a frio
possuem particularidades, tais como a necessidade de cuidados adicionais na
execução das ligações e, principalmente, a susceptibilidade ao modo local e ao
modo distorcional de flambagem. A Figura 1 apresenta a seção U enrijecido,
bastante comum em perfis formados a frio.
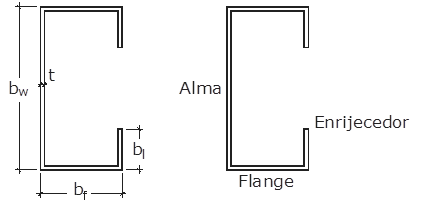
Figura 1: Seção U enrijecido, onde bw é a largura da alma, bf
a largura da mesa, bl a largura do enrijecedor e t a espessura.
O modo local
apresenta maior probabilidade de ocorrência do que em perfis laminados ou
soldados devido à elevada esbeltez das chapas que constituem a seção [1]. Já o modo distorcional
caracteriza-se pela rotação da mesa e do enrijecedor em relação à alma,
ocasionando o fechamento ou a abertura do pilar. Como o modo distorcional não
apresenta resistência pós crítica, a sua ocorrência pode levar a colapsos
bruscos e, consequentemente, a tragédias [2]. A Figura 2 apresenta os modos local e distorcional na seção
U enrijecido.
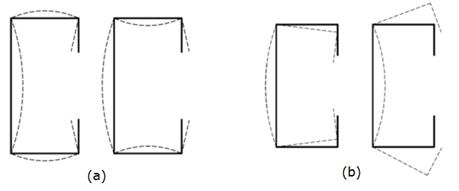
Figura 2: (a) Modo local na seção U enrijecido; (a)
Modo distorcional.
A determinação
da resistência de uma estrutura de aço em perfis formados a frio sujeita à
flambagem local e à flambagem global, considerando inclusive a interação entre
os modos, pode ser feita pelo tradicional Método da Largura Efetiva, que visa
quantificar a redução da resistência ocasionada pela flambagem local
descontando da largura da chapa a região afetada pelo fenômeno. Este método foi
desenvolvido por Winter em 1947 e por muito tempo mostrou-se suficiente para a
previsão do comportamento e da resistência de perfis formados a frio [2].
No entanto, o
advento de seções mais complexas, contando com enrijecedores, além da adoção de
tipos de aço com elevadas tensões de escoamento mostraram o surgimento do modo
distorcional, que não obedece às premissas do Método da Largura Efetiva [3]. O tratamento analítico deste modo de
flambagem inicialmente mostrou-se muito complexo, inviável para fins de
utilização em escritórios de projeto. Assim, o dimensionamento de perfis
sujeitos ao modo distorcional tem sido feito pelo Método da Resistência Direta [4] [5], que atualmente se encontra prescrito
em diversas normas de projeto, tais como a americana AISI-S100-16 [6], a australiana AS/NZS 4600 [7] e a brasileira NBR 14762 [8]. Ressalta-se que o Método da Resistência Direta é
muito abrangente, sendo adequado para a previsão da flambagem local, da
flambagem distorcional e da flambagem global, podendo considerar inclusive suas
interações, com uma quantidade reduzida de cálculos. Possui, no entanto a
necessidade de que seja feita a análise de estabilidade da seção, o que pode
ser feito, por exemplo, pela Teoria Generalizada de Vigas (GBT) pelo software
GBTul [9].
Buscando
aumentar a praticidade da utilização de perfis formados a frio, em diversas
aplicações é comum sua fabricação com perfurações, que visam a passagem de
instalações e o encaixe de ligações. Diversos estudos indicam a possibilidade
de adaptação do Método da Resistência Direta para a avaliação da resistência de
perfis formados a frio com perfurações [10-13]. A norma americana [6] traz em seu escopo prescrições para a previsão das
perfurações baseadas no trabalho de Moen e Schafer [14], enquanto a norma brasileira [8] ainda não o traz.
Neste
contexto, este trabalho tem o objetivo de contribuir com a possibilidade de adaptação
do Método da Resistência Direta para a análise da resistência de perfis
formados a frio do tipo U enrijecido com perfurações, considerando a flambagem
distorcional, avaliando métodos desenvolvidos em trabalhos anteriores [11] [14] para diferentes seções e arranjos de
perfurações. Também será avaliada a influência da variação das dimensões das
perfurações na resistência destas estruturas. A metodologia adotada será a
comparação de resultados obtidos com o Método da Resistência Direta adaptado
com resultados de referência obtidos a partir de modelos numéricos via
elementos finitos pelo software ANSYS [15], cujo procedimento foi validado experimentalmente em
trabalhos anteriores [16, 17].
2
Método
da Resistência Direta
2.1
Perfis
sem perfurações
O Anexo C da norma ABNT NBR 14762 [8] apresenta as prescrições do Método da Resistência Direta
para o cálculo da força axial de compressão resistente para perfis formados a
frio sujeitos à flambagem distorcional sem perfurações (Nc,Rdist),
conforme apresentado na Equação 1.
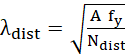
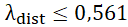 ,
, 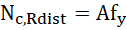 (1)
(1)
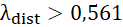 ,
, 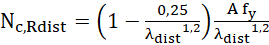
Em que A é a área bruta da seção, fy é a tensão de escoamento
do material e Ndist é a força axial de flambagem distorcional
elástica, obtida pela análise de estabilidade da seção no software GBTul. Este
programa fornece a curva de assinatura da seção. A partir dela, é possível
determinar a força axial de flambagem distorcional elástica no segundo mínimo,
e o comprimento da coluna a ela associado, no eixo das abscissas, conforme
apresentado na Figura 3.
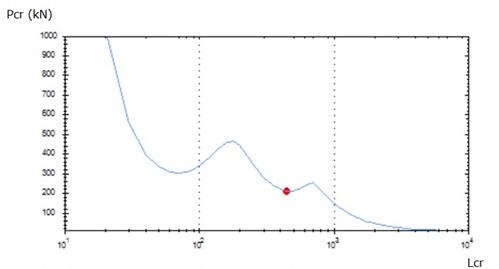
Figura 3: Curva de assinatura obtida no GBTul,
destacando-se a força axial de flambagem distorcional elástica (Ndist = 209,68 kN) e o
comprimento a ela associado (L = 450 mm).
Ressalta-se que a análise de estabilidade elástica feita no software
GBTul é limitada a perfis sem perfurações, advindo daí a necessidade de
adaptações que considerem seu efeito nos pilares.
2.2
Perfis
com Perfurações – MOEN
Visando considerar a redução da rigidez da alma da seção devido à
existência de perfurações, Moen e Schafer [17] apresentaram propostas de adaptação do Método da
Resistência Direta para pilares perfurados, conforme apresentado na Equação 2.
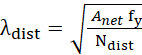
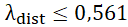 ,
, 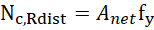 (2)
(2)
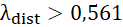 ,
, 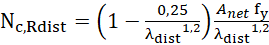
Onde percebe-se a substituição da área bruta, A, pela área líquida, Anet,
nas equações. Além desta mudança, inserem-se também modificações na
determinação da força axial de flambagem distorcional elástica (Ndist)
feita pelo software GBTul, substituindo-se a espessura da alma t (Figura 1)
pela espessura reduzida tweb,hole, calculada pela equação 3.
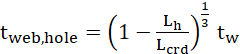 (3)
(3)
Onde tw é a espessura real da alma, Lh é o
comprimento do furo e Lcrd é o comprimento crítico distorcional para
a seção sem perfurações, obtido via GBTul como mostrado na Figura 3.
2.3
Perfis
com Perfurações – Sales
Alternativamente à proposta de Moen e Schafer, Sales [11] avaliou a substituição da espessura
real da alma pela espessura fictícia tfic na determinação da força
axial de flambagem distorcional elástica (Ndist) feita pelo software
GBTul, conforme indicado na Equação 4.
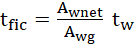 (4)
(4)
Onde tw é a espessura real da alma, Awnet é a área
da alma descontadas as perfurações e Awg é a área bruta da alma.
Para a determinação da força axial de compressão resistente para perfis
formados a frio sujeitos à flambagem distorcional (Nc,Rdist), é
utilizada a Equação 2, modificando-se, portanto, apenas a análise elástica via
GBTul.
Estes métodos foram utilizados para a análise de perfis formados a frio
com perfurações e tiveram seus resultados comparados a resultados numéricos
obtidos por um modelo de elementos finitos previamente calibrado
experimentalmente.
3
Análise
numérica
Para avaliar a influência das dimensões das perfurações, foram
selecionadas 16 seções do tipo U enrijecido cujas dimensões são apresentadas na
Tabela 1.
A escolha destas dimensões foi feita de forma a garantir a ocorrência da
flambagem distorcional nestas seções. Cada uma destas seções foi analisada sem
perfurações e com perfurações, como apresentado na Figura 4, com o comprimento
do furo, hf, sendo adotado como 20%, 40%, 60% e 80% de bw.
Foram consideradas dois tipos diferentes de propriedades elastoplásticas do
aço: a tensão de escoamento (fy) igual a 220 MPa e a tensão última
(fu) igual a 328 MPa, obtidos experimentalmente [16]; e a tensão de escoamento (fy) igual a 300 MPa e a
tensão última (fu) igual a 490 MPa, do aço CF-30 previsto em norma [8]. Estas propriedades foram inseridas
no modelo por meio de uma aproximação multilinear do diagrama tensão x
deformação [17]. Os comprimentos dos modelos foram
obtidos a partir dos comprimentos críticos obtidos via GBTul, sem considerar a
existência de perfurações, como indicado na Figura 2.
Tabela 1: Dimensões das seções U enrijecido.
|
Dimensões em mm (bw x bf x bl x
t)
|
|
|
|
GRUPO 50
|
Ue
50x45x10x1,2
|
|
|
Ue
50x45x10x1,4
|
|
|
Ue
50x45x10x1,6
|
|
|
Ue
50x45x10x1,8
|
|
|
Ue
50x45x10x2,0
|
|
|
GRUPO 68
|
Ue
68x68x20x2,2
|
|
|
Ue
68x68x20x2,4
|
|
|
Ue
68x68x20x2,6
|
|
|
Ue
68x68x20x2,8
|
|
|
GRUPO 75
|
Ue
75x65x15x1,6
|
|
|
Ue
75x65x15x1,8
|
|
|
Ue
75x65x15x2,0
|
|
|
Ue
75x65x15x2,2
|
|
|
Ue
75x65x15x2,4
|
|
|
GRUPO 100
|
Ue
100x100x20x2,2
|
|
|
Ue
100x100x20x2,4
|
|
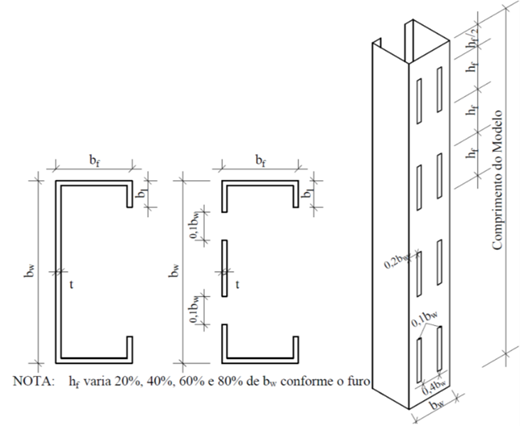
Figura 4: Geometria das seções e arranjo das perfurações
adotadas.
Para a construção do modelo numérico no ANSYS foi utilizado o elemento
SHELL181, com elementos quadrangulares com lado igual a 10% da largura da alma
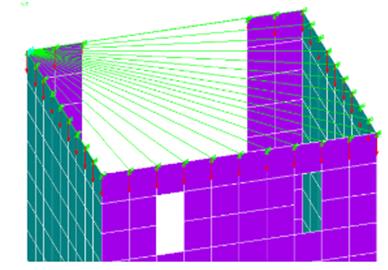
(bw). As condições de contorno adotadas foram a restrição dos
deslocamentos nas direções ortogonais aos eixos nas extremidades associada ao
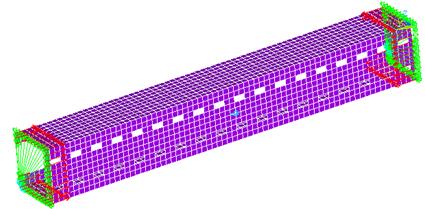
acoplamento de todos os deslocamentos nestes nós (Figura 5(a)). Foi ainda
restringido o deslocamento na direção axial do modelo em nó à meia altura, a
fim de evitar o deslocamento de corpo rígido (Figura 5(b)).
O carregamento
foi aplicado de forma distribuída, por meio da aplicação de uma componente em
cada nó da aresta da extremidade, tomando-se a precaução de aplicar no nó
extremo metade do valor aplicado nos outros nós devido à sua menor área de
influência, conforme apresentado na Figura 6.
(a)
(b)
Figura 5: Condições de contorno (a) extremidade; (b)
modelo completo.
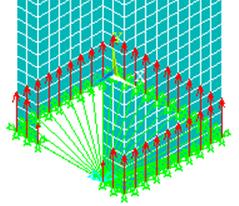
Figura 6: Aplicação do carregamento.
A análise numérica foi feita em duas etapas. Primeiramente, foi feita a
análise de autovalor, e obtido o modo distorcional. A partir destes
deslocamentos, foi introduzido um fator de imperfeição igual à metade da
espessura, e feita a análise não-linear física e geométrica, sendo obtida a
força axial de compressão resistente de cada modelo via ANSYS. Esse modelo foi
validado em termos de capacidade de carga e de modo de falha a partir de
comparações com dados experimentais em estudos anteriores [16], [17], conforme mostra a Figura 7. Assim,
os resultados numéricos foram usados como referência para a validação da
aplicação das modificações do Método da Resistência Direta para as várias
configurações de perfurações analisadas, bem como para a análise da influência
das dimensões das perfurações na resistência das seções estudadas.
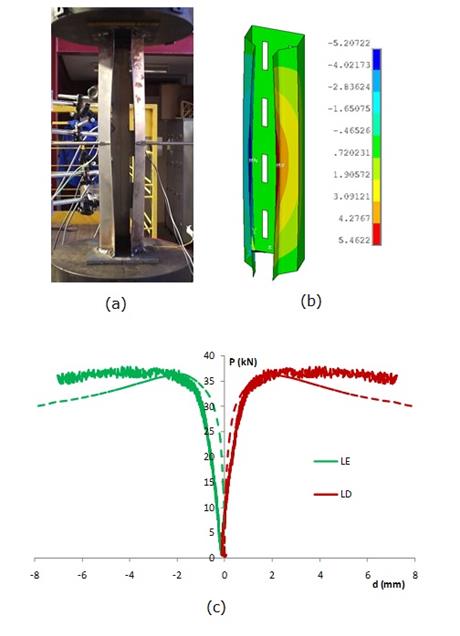
Figura 7: Validação do modelo numérico: (a)
Deslocamentos do protótipo experimental; (b) Deslocamentos do modelo numérico;
(c) Curvas carga x deslocamento experimental (linha cheia) e numérica (linha
tracejada) [16].
4
Resultados
Para avaliar a
eficiência das modificações propostas para considerar as perfurações no Método
da Resistência Direta, os resultados do modelo numérico foram comparados com
resultados analíticos para demonstrar a sua eficiência. As Figura 8 e 9
apresentam os resultados considerando a aproximação proposta por Sales, onde a
curva apresenta os resultados teóricos e os pontos apresentam os resultados
obtidos pelo método dos elementos finitos. As figuras 9 e 10 apresentam os
resultados considerando-se o método proposto por Moen e Schafer para a
consideração das perfurações.
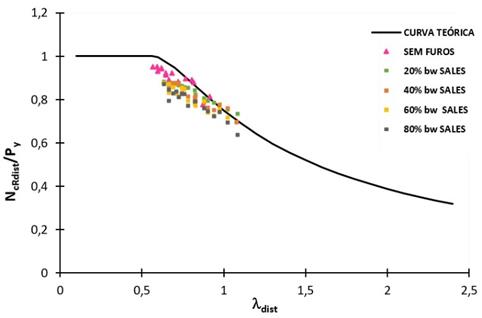
Figura 8: Comparação de resultados analíticos e
numéricos, considerando fy = 220 MPa e o método de Sales (Py
= Afy).
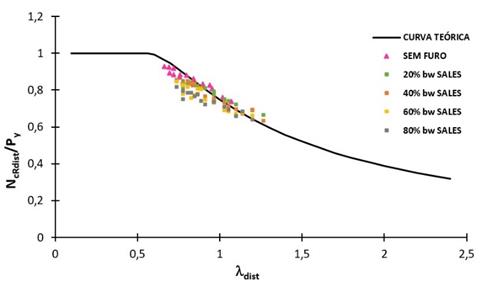
Figura 9: Comparação de resultados analíticos e
numéricos, considerando fy = 300 MPa e o método de Sales (Py
= Afy).
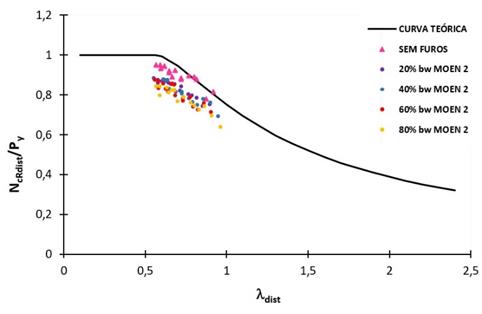
Figura 10: Comparação de resultados analíticos e
numéricos, considerando fy = 220 MPa e o método de Moen (Py
= Afy).
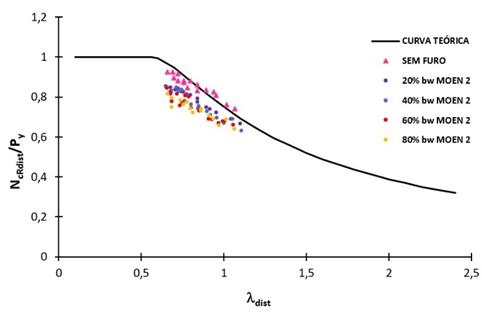
Figura 11: Comparação de resultados analíticos e
numéricos, considerando fy = 300 MPa e o método de Moen (Py
= Afy).
Nas figuras 8
a 11 pode-se observar que, para as duas tensões de escoamento consideradas
existe uma correlação adequada entre os resultados numéricos e analíticos,
indicando a validade das adaptações do Método da Resistência Direta avaliadas.
Observa-se ainda que existe uma redução das resistências dos pilares com
perfurações em relação àqueles sem elas, como era inicialmente esperado. A
Tabela 2 apresenta as relações entre os resultados do Método da Resistência
Direta e do ANSYS, podendo-se ver que a máxima diferença é de 11% para a
aproximação de Sales e de 18% para a aproximação de Moen.
A partir da
análise das Figuras 7-10 e da Tabela 2 pode-se observar que os ajustes teóricos
no método da resistência direta levam a bons resultados, indicando a
viabilidade da aplicação destes métodos para fins de projeto.
Tabela 2: Relações entre o Método da Resistência
Direta Adaptado e o Método dos Elementos Finitos.
|
TIPO
|
fy
|
MÉDIA
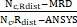
|
DESVIO
PADRÃO
|
|
(MPa)
|
|
SEM
FUROS
|
220
|
1,04
|
0,032
|
|
300
|
1,01
|
0,037
|
|
|
SALES
|
MOEN
|
SALES
|
MOEN
|
|
20% bw
|
220
|
1,05
|
1,12
|
0,046
|
0,021
|
|
300
|
1,00
|
1,10
|
0,048
|
0,032
|
|
40% bw
|
220
|
1,06
|
1,14
|
0,043
|
0,027
|
|
300
|
1,02
|
1,12
|
0,041
|
0,030
|
|
60% bw
|
220
|
1,03
|
1,17
|
0,041
|
0,032
|
|
300
|
1,06
|
1,15
|
0,048
|
0,041
|
|
80% bw
|
220
|
1,11
|
1,18
|
0,043
|
0,030
|
|
300
|
1,08
|
1,17
|
0,055
|
0,044
|
Foi feita
ainda a análise da influência das perfurações na resistência dos pilares. As
Figura 12 e 13 apresentam a redução percentual entre as resistências dos
pilares perfurados em relação aos pilares sem perfurações, para todas as
seções analisadas. Observa-se que a existência das perfurações leva a uma
redução da resistência das colunas. Pode-se ainda observar que, para a maioria
das seções analisadas, o aumento do comprimento das perfurações leva a uma
maior redução da resistência, apesar de não obedecer a um padrão específico
para a maioria das seções. A Tabela 3 apresenta as médias e desvios padrões
percentuais das resistências dos pilares com perfurações em relação àqueles sem
elas.
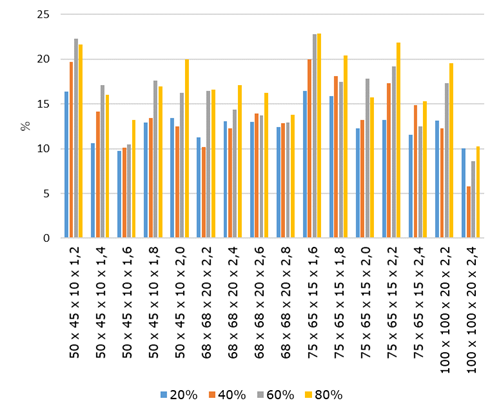
Figura 12: Redução percentual entre as resistências
obtidas no ANSYS dos pilares com perfurações em relação aos pilares sem
perfurações para fy = 220 MPa.
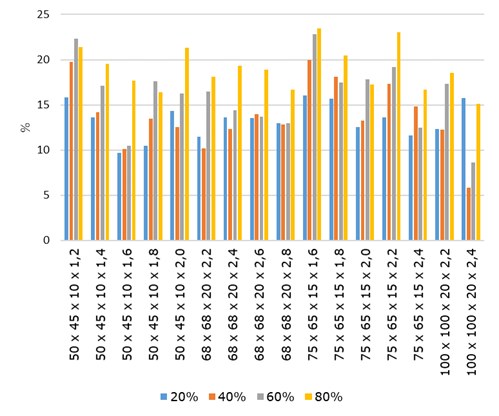
Figura 13: Redução percentual entre as resistências
obtidas no ANSYS dos pilares com perfurações em relação aos pilares sem perfurações
para fy = 300 MPa.
Tabela 3: Média e desvio padrão das reduções
percentuais de resistência dos pilares com perfurações em relação àqueles sem
perfurações.
|
fy
(MPa)
|
Altura
do Furo
|
MÉDIA (%)
|
DESVIO
PADRÃO (%)
|
|
220
|
20% bw
|
12,84
|
1,97
|
|
40% bw
|
13,80
|
3,57
|
|
60% bw
|
16,06
|
3,73
|
|
80% bw
|
17,36
|
3,37
|
|
300
|
20% bw
|
13,31
|
1,88
|
|
40% bw
|
15,06
|
3,01
|
|
60% bw
|
17,54
|
3,33
|
|
80% bw
|
18,99
|
2,35
|
A partir da
análise destes resultados, observa-se que maiores perfurações levam a maiores
reduções na resistência quando se usa como referência o caso sem perfurações,
apesar deste comportamento não apresentar um padrão específico.
Observa-se
ainda que a adoção de um aço com maior tensão de escoamento leva a uma redução
ligeiramente maior. Isto pode ser explicado pois, neste caso, o modo
distorcional pode se desenvolver com mais liberdade antes da ruptura por escoamento,
o que pode fazer com que os efeitos das perfurações sejam mais relevantes.
5.
Conclusões
Este
trabalho analisou a eficiência das adaptações do Método da Resistência Direta
para a previsão da Resistência de perfis formados a frio do tipo U enrijecido
com perfurações e a influência das dimensões destes furos na resistência destas
estruturas, tomando como referência resultados numéricos obtidos em um modelo
previamente validado a partir de resultados experimentais.
Observou-se
que as adaptações do Método da Resistência Direta se mostraram promissoras na
previsão do comportamento destas estruturas, considerando-se a prevalência do
modo de flambagem distorcional, com diferenças máximas de 11% para a
aproximação de Sales e de 18% para a aproximação de Moen.
Foi ainda
avaliada a redução da resistência devido à inserção das perfurações nos
pilares. Estas análises indicaram que os furos diminuem a resistência dos
pilares, com reduções entre 13% e 19%, sendo tanto maior quanto maiores forem
as dimensões das perfurações.
Referências
[1] YU, W. Cold formed steel design. 3rd ed. New York: John Wiley &
Sons, 2000.
[2] SCHAFER, B.W. Advances in the Direct Strength Method
of cold-formed steel design. Thin-Walled Structures 140, páginas 533-541, 2019.
https://doi.org/10.1016/j.tws.2019.03.001
[3] HANCOCK, G. J.; KWON, Y. B.; BERNARD, E. S.
Strength design curves for thin-walled sections undergoing distortional
buckling. Journal of Constructional Steel Research, v. 31, nº. 2-3, p. 169-186,
1994.
[4] SCHAFER, B.W. Review: the direct strength melhod of
cold-formed steel member design. Journal of Constructional Steel Research, v.
64, p. 766-778, 2008.
[5] CAMOTIM, D., DINIS, P.B. MARTINS, A.D. Direct strength
method a general approach to the design of cold-formed steel members, in: C. Yu
(Ed.), Recent Trends in Cold-Formed Steel Construction, 2016.
[6] AISI – American Iron and Steel Institute.
North American Specification (NAS) for the Design of Cold-Formed Steel
Structural Members (AISI-S100-16). Washington DC: AISI, 2016.
[7] AS/NZS. Cold-formed steel structures (AS/NZS
4600:2018). Superseding AS/NZS 4600:2005 on 15 May 2019. Sydney-Wellington: AS/NZS, May 15th 2018.
[8] ABNT – Associação Brasileira de Normas Técnicas. ABNT NBR 14762:
Dimensionamento de estruturas de aço constituídas por perfis formados a frio. Rio de Janeiro: ABNT, 2010.
[9] BEBIANO, R., SILVESTRE, N., CAMOTIM, D.
GBTUL - A code for the buckling analysis of cold-formed steel members. In:
INTERNATIONAL SPECIALTY CONFERENCE ON COLD-FORMED STEEL STRUCTURES, 19., 2008,
St. Louis (MO). Proceedings. St. Louis
(MO): p. 61-79, Oct. 14 and 15 2008.
[10] SOUZA, F. T., SANTOS, E. T., SARMANHO, A. M. C. Análise numérica da
influência das dimensões de perfurações em perfis formados a frio do tipo rack
submetidos à compressão. Revista Mundi Engenharia, Tecnologia e Gestão,
Paranaguá, PR, v. 5, n. 5, p. 266-01, 266-20, 2020.
[11] SALES, A. E. C. A. Análise da aplicação do método da resistência direta
a perfis formados a frio com perfurações submetidos à compressão. Dissertação
(Mestrado Profissional em Construção Metálica) - Escola de Minas, Departamento
de Engenharia Civil, Universidade Federal de Ouro Preto (UFOP), Ouro Preto,
2017.
[12] JARDIM JÚNIOR, F. Estudo da viabilidade do método da
resistência direta em perfis U enrijecidos formados a frio com perfurações.
Dissertação (Mestrado em Engenharia Civil) – Escola de Minas, Departamento de
Engenharia Civil, Universidade Federal de Ouro Preto (UFOP), Ouro Preto, 2018.
[13] SANTOS, E. T. Análise numérica da influência das dimensões das
perfurações em perfis formados a frio do tipo rack submetidos à compressão.
Dissertação (Mestrado profissional em Construção Metálica) – Escola de Minas,
Departamento de Engenharia Civil, Universidade Federal de Ouro Preto (UFOP),
Outro Preto, 2020.
[14]
MOEN, C. D.; SCHAFER, B. W.
Direct Strength Design of Cold‐Formed Steel members with perforations: Research Report RP 09-1. Washington:
American Iron and Steel Institute – Committee on Specifications for the Design
of Cold-Formed Steel Strutuctural Members, 2009.
[15] SWANSON ANALYSIS SYSTEMS INC. ANSYS. Vs. 14.5. Houston, USA: 2020.
[16] SOUZA, F. T. Análise teórico-experimental da
estabilidade de colunas perfuradas em perfis de aço formados a frio de seções
tipo rack. Tese (Doutorado em Engenharia Civil) – Escola de Minas, Departamento
de Engenharia Civil, Universidade Federal de Ouro Preto (UFOP), Ouro Preto,
2013.
[17] FARIA, V. O. Análise de estabilidade de perfis formados a frio com
perfurações. Dissertação (Mestrado em Engenharia Civil) – Escola de Minas,
Departamento de Engenharia Civil, Universidade Federal de Ouro Preto (UFOP),
Ouro Preto, 2016.
orcid.org/0000-0002-6303-6233
orcid.org/0000-0001-6900-8551
orcid.org/0000-0003-3261-9089