1 INTRODUÇÃO
Na indústria automotiva,
onde a eficiência é crucial para a competitividade em um mercado em constante
evolução, o consumo de energia emerge como uma preocupação estratégica de
grande relevância. As oficinas de pintura representam uma parcela significativa
do consumo energia em fábricas automotivas, muitas vezes variando de 50% a 70%
do consumo total de produção [1].
Especificamente, a eletricidade e o gás natural surgem como os principais
vetores energéticos consumidos ao longo dos diversos estágios do processo de
pintura, que incluem desde o pré-tratamento da superfície até a fase de secagem
e cura do revestimento [2].
A otimização do consumo de
energia na pintura automotiva é crucial para reduzir custos e o impacto
ambiental, promovendo a sustentabilidade e competitividade do setor.
1.1 DESCRIÇÃO DO PROBLEMA
A previsão e gestão do
consumo de energia em oficinas de pintura automotiva são impactadas pela complexidade
dos processos e pela falta de dados precisos sobre os fatores que influenciam o
consumo. Contudo, o crescente interesse no desenvolvimento de modelos de
previsão de consumo de energia, utilizando métodos de Aprendizado de Máquina (do
inglês Machine Learning - ML), Aprendizado Profundo (do inglês Deep
Learning - DL) [3] e de
algoritmos metaheurísticos para otimizar o resultado desses modelos oferece
oportunidades para aprimorar a eficiência energética e operacional na indústria
automotiva.
A utilização dos modelos de
ML ou DL como learning fitness functions (aprendizado como função de aptidão)
nos algoritmos metaheurísticos potencializa ainda mais a busca por soluções
eficazes. [4].
Estudos têm aplicado
técnicas como a Floresta Aleatória (do inglês Random Forest - RF) [5] e XGBoost [6]
na previsão do consumo de energia na indústria. RF é uma técnica de ensemble
que utiliza múltiplas árvores de decisão para realizar previsões mais robustas.
O XGBoost, baseado em árvores de decisão, constrói iterativamente várias
árvores para corrigir os erros das anteriores.
Em DL, modelos baseados em
redes neurais recorrentes, como a rede neural Memória de longo prazo (do inglês
Long Short Term Memory - LSTM), têm sido amplamente utilizados devido à
sua capacidade de capturar padrões temporais complexos nos dados de consumo de
energia [7]. Além disso, abordagens
híbridas que incluem o framework Prophet e Rede Neural Recorrente (do inglês Recurrent
Neural Network - RNN) têm se mostrado promissoras em análises baseadas em
séries temporais [8], resultando em
previsões mais precisas e insights mais profundos sobre o comportamento do
consumo de energia em oficinas de pintura [9].
1.2 JUSTIFICATIVA
A previsão do consumo
energético na indústria automotiva permite otimizar processos, reduzir custos e
programar operações de alta demanda, como a secagem em oficinas de pintura [10].
Os estudos sobre
sustentabilidade na indústria automotiva destacam a crescente importância desse
tema, revelando tanto desafios quanto oportunidades para as empresas do setor.
Szász et al. [11] e
Lukin et al. [12] destacam a
crescente importância da sustentabilidade na indústria automotiva e a busca por
estratégias para cumprir os objetivos de desenvolvimento sustentável da ONU. Portanto,
é necessário um estudo que otimize o consumo energético e ciclo de produção na
indústria automotiva, visando eficiência energética, sustentabilidade e
eficiência operacional.
1.3 OBJETIVOS
Este trabalho tem como
objetivo prever o consumo energético e maximizar o ciclo de produção em um
ambiente de pintura automotiva a partir de uma arquitetura de 3 steps,
utilizando técnicas de ML, DL e algoritmos meta-heurísticos.
2
FUNDAMENTAÇÃO TEÓRICA
Esta fundamentação teórica fornece
base sólida para identificar o estado da arte da análise do consumo energético
em oficinas de pintura automotiva e apresentar as técnicas utilizadas na
metodologia a partir de
2.1 TRABALHOS RELACIONADOS
Pesquisadores exploram
técnicas como mineração de dados, ML e DL para otimizar o consumo energético em
oficinas de pintura automotiva. Cavalcante et al. [13]
propôs uma metodologia para ajustar o modelo matemático capaz de prever o
comportamento do processo de cura de tintas, determinando coeficientes de
transferência de calor com base em dados industriais, com os resultados
indicando o modelo como uma ferramenta promissora para desenvolver estratégias
de otimização operacional, além de minimizar retrabalhos e custos de energia.
Lu et al. [9] traz uma abordagem baseada em ML híbrida,
onde o modelo Prophet ajusta as características cíclicas e de tendência dos
dados, o EEMD (Ensemble Empirical Mode Decomposition) decompõe os
resíduos e melhora a sensibilidade do modelo, enquanto a LSTM captura as
características temporais dos dados. Os resultados experimentais evidenciaram o
alto desempenho preditivo do modelo Prophet-EEMD-LSTM, com valor médio de 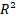 0,94006.
0,94006.
Hovgard [14] investigou a redução do uso de energia em
estações robóticas em linhas de produção automotiva por meio de otimização
estocástica, resultando em redução de até 23% do consumo de energia sem grande
impacto na variação do tempo de ciclo de produção. Indo além da indústria
automotiva, Ilbeigi et al. [15]
propôs um método para otimizar o consumo de energia em edifícios por meio de
uma abordagem que combina modelagem com o software EnergyPlus, uma rede neural
artificial (RNA) e otimização com Algoritmo Genético (do inglês Genetic
Algorithm - GA). Os resultados demonstram uma redução de cerca de 35% no
consumo de energia após a otimização do sistema.
A maioria das pesquisas
sobre previsão de consumo energético busca modelos preditivos para otimizar a
relação entre oferta e demanda. Por outro lado, na otimização do consumo de
energia, os estudos se concentram na resolução de problemas de otimização,
buscando insumos ideais para melhorar a eficiência energética [16].
Essas abordagens inovadoras
melhoram a eficiência energética e a sustentabilidade no setor. Esta pesquisa
se diferencia por aplicar uma arquitetura de 3 etapas integrando ML, DL e
algoritmos metaheurísticos para buscar ainda mais otimizar o consumo de energia.
2.2 MODELO
HÍBRIDO GRU-LSTM
À medida que a complexidade
da modelagem de sequências aumenta, surge a necessidade de abordagens mais
eficazes. Entre as técnicas exploradas estão as RNNs, e suas variantes Unidade
Recorrente Fechada (do inglês Gated Recurrent Unit - GRU) e LSTM. Embora
eficazes em dados sequenciais, GRUs e LSTMs apresentam limitações: GRUs
oferecem maior eficiência computacional, mas podem ter dificuldade em capturar
dependências de longo prazo, enquanto LSTMs, apesar de mais poderosas nesse
aspecto, demandam maior custo computacional. [17][18].
A integração de GRU e LSTM
visa criar um modelo eficiente e capaz de capturar informações relevantes. A
GRU filtra informações capturando padrões de curto prazo, que são passadas para
a LSTM as integrar ao contexto histórico para modelagem precisa de sequências
complexas.
No contexto da previsão de
consumo de energia em oficinas de pintura automotiva, uma arquitetura híbrida com
GRU e LSTM, assim como em outras produções científicas semelhantes, pode ajudar
a capturar tanto os padrões de consumo de curto prazo, relacionados a
flutuações diárias ou semanais, quanto as tendências de longo prazo, associadas
a mudanças sazonais ou de produção [19][20].
2.2.1
Memória de Longo Prazo
A LSTM foi introduzida pela
primeira vez por Sepp Hochreiter e Jurgen Schmidhuber em 1997 [21]. É um tipo especializado de RNN
desenvolvida para lidar com sequências de dados e capturar dependências
temporais de longo prazo. Em comparação com redes neurais tradicionais, as
LSTMs possuem uma arquitetura mais complexa, incorporando unidades de memória
interna chamadas de células. Essas células são capazes de armazenar informações
ao longo do tempo e controlar o fluxo de informações na rede, permitindo que as
LSTMs mantenham e atualizem estados de memória por longos períodos.
Uma célula LSTM os
seguintes componentes: uma porta de entrada 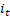 , porta de esquecimento
, porta de esquecimento 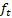 , porta de saída
, porta de saída 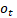 , estado de célula
candidata
, estado de célula
candidata 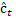 , estado de célula
, estado de célula 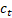 e um estado oculto
e um estado oculto 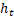 , dado pelas Equações (1),
(2), (3), (4), (5) e (6), respectivamente. A função da porta de entrada é determinar
quais informações devem ser armazenadas no estado de célula atual, enquanto a
porta de esquecimento identifica as informações que devem ser descartadas. Por
fim, a porta de saída determina quais informações serão transmitidas para o
estado oculto atual.
, dado pelas Equações (1),
(2), (3), (4), (5) e (6), respectivamente. A função da porta de entrada é determinar
quais informações devem ser armazenadas no estado de célula atual, enquanto a
porta de esquecimento identifica as informações que devem ser descartadas. Por
fim, a porta de saída determina quais informações serão transmitidas para o
estado oculto atual.
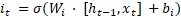 (1)
(1)
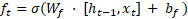 (2)
(2)
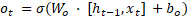 (3)
(3)
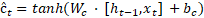 (4)
(4)
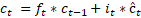 (5)
(5)
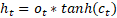 (6)
(6)
Onde 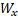 e
e 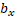 representam a matriz de
pesos e o vetor de bias de cada equação, respectivamente.
representam a matriz de
pesos e o vetor de bias de cada equação, respectivamente.
2.2.2
Unidade Recorrente Fechada
GRU é uma arquitetura que
pertence à família das RNNs. Assim como a LSTM, a GRU é projetada para lidar
com problemas de sequência, onde a entrada ou saída é uma sequência de dados,
como em tradução de texto, previsão de séries temporais, entre outros. A GRU
possui duas portas principais: update gate e reset gate. A update gate controla
quanto do estado anterior deve ser mantido e quanto do novo estado proposto
deve ser adicionado. Enquanto isso, a reset gate decide quanto do estado
anterior deve ser esquecido.
Essas portas permitem que a
GRU aprenda a memorizar informações importantes de maneira mais eficiente do
que as RNNs tradicionais. Além disso, as GRUs tendem a ser mais fáceis de
treinar e mais eficientes computacionalmente, pois possuem menos parâmetros.
2.3
ALGORITMOS META-HEURÍSTICOS
Meta-heurísticas são
abordagens de resolução de problemas de otimização que não garantem a solução
ótima, mas buscam encontrar boas soluções em um tempo computacionalmente
viável. Essas técnicas exploram o espaço de busca de forma genérica e
adaptativa, sendo aplicáveis a uma variedade de problemas complexos [22].
2.3.1
Otimização por Enxame de Partículas
A Otimização por Enxame de
Partículas (do inglês Particle Swarm Optimization - PSO) é uma técnica
de otimização computacional baseada em simulação de enxame, inspirada no
comportamento de pássaros e cardumes de peixes. A ideia central do PSO é
simular o comportamento de um grupo de partículas, cada uma representando uma
solução candidata para o problema de otimização. Cada partícula se move pelo
espaço de busca, ajustando sua posição e velocidade de acordo com seu próprio
histórico de desempenho e o desempenho do grupo como um todo [23].
A atualização da velocidade
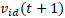 de uma partícula
de uma partícula 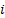 de dimensão
de dimensão 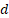 , na iteração
, na iteração 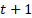 é calculada pela equação 9
e sua posição
é calculada pela equação 9
e sua posição 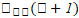 é dada pela equação 10.
é dada pela equação 10.
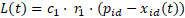 (7)
(7)
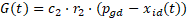 (8)
(8)
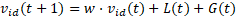 (9)
(9)
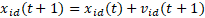 (10)
(10)
Onde 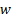 é o coeficiente de
inércia,
é o coeficiente de
inércia, 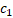 e
e 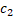 são os coeficientes que
controlam a influência do melhor valor pessoal e global, respectivamente,
são os coeficientes que
controlam a influência do melhor valor pessoal e global, respectivamente, 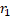 e
e 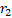 são números aleatórios
entre 0 e 1,
são números aleatórios
entre 0 e 1, 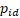 e
e 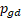 são as melhores posições
já alcançadas pela partícula i e pelo enxame até o momento, respectivamente.
são as melhores posições
já alcançadas pela partícula i e pelo enxame até o momento, respectivamente. 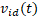 e
e 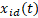 descrevem a velocidade e a
posição da partícula
descrevem a velocidade e a
posição da partícula 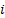 na dimensão
na dimensão 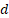 na iteração atual
na iteração atual 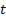 , respectivamente.
, respectivamente.
2.3.2
Evolução Diferencial
O algoritmo Evolução
Diferencial (do inglês Differential Evolution - DE) é um método de
otimização baseado em população, inspirado no processo de evolução natural.
Opera em uma população de vetores, onde cada vetor representa uma solução
candidata para o problema de otimização em questão [24].
O algoritmo começa gerando
aleatoriamente uma população inicial de soluções (vetores) candidatas dentro do
espaço de busca. Cada vetor passa por uma mutação diferencial, onde um vetor
mutante é gerado combinando diferenças ponderadas entre três vetores
selecionados aleatoriamente da população. A mutação é realizada pela seguinte
equação:
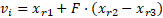 (11)
(11)
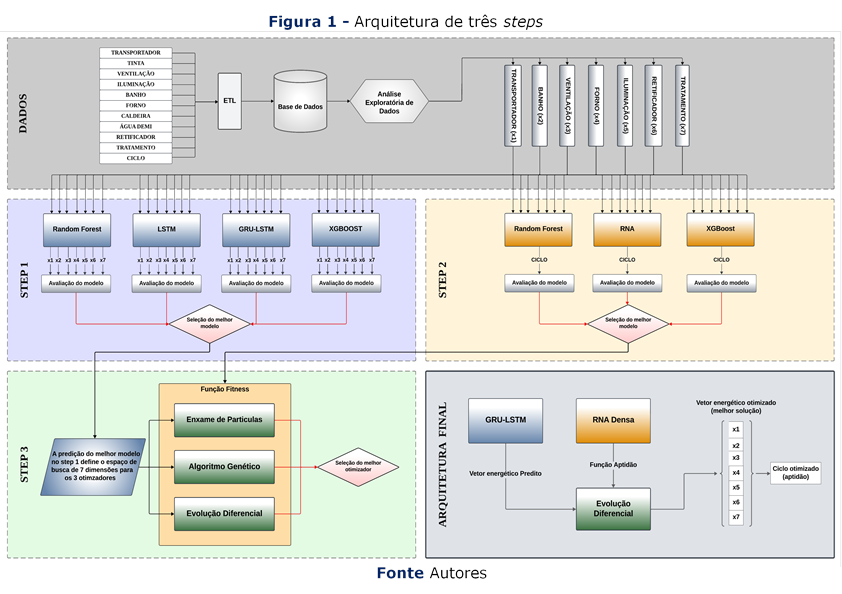
Onde 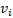 é o novo vetor mutante
gerado para o indivíduo i na geração g,
é o novo vetor mutante
gerado para o indivíduo i na geração g, 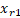 ,
, 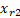 e
e 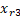 são três vetores distintos
selecionados aleatoriamente da população atual, exceto o próprio indivíduo i.
F é um parâmetro de controle chamado de fator de escala, que controla o
grau de perturbação aplicado à diferença entre os vetores selecionados.
são três vetores distintos
selecionados aleatoriamente da população atual, exceto o próprio indivíduo i.
F é um parâmetro de controle chamado de fator de escala, que controla o
grau de perturbação aplicado à diferença entre os vetores selecionados.
Na etapa de cruzamento,
vetores mutantes são combinados com os vetores originais. Em seguida, na seleção,
os novos vetores resultantes são avaliados em relação aos originais. Se um
vetor mutante for melhor, substitui o original na próxima geração, caso
contrário, o vetor original é mantido. O DE segue os passos de mutação,
cruzamento e seleção por várias gerações até que um critério de parada seja
atingido.
3 MATERIAL E MÉTODOS
As
especificações dos modelos, dados e métricas utilizados na pesquisa estão
descritos a seguir.
3.1 BASE DE DADOS E PRÉ-PROCESSAMENTO
O dataset
desta pesquisa é o mesmo utilizado no estudo de Oliveira et al. [25] e suas características são:
●
Extração,
Transformação e Carga (do inglês Extract, Transform and Load - ETL) de
bases de dados - Dados de energia e de produção de veículos.
●
As
variáveis de entrada nos modelos deste estudo são os processos da oficina de
pintura, contendo dados de kWh.
●
As
variáveis de saída do step 1 são as 7 variáveis de entrada em t+1 e para
os modelos do step 2 é o ciclo (produtividade de veículos na oficina de
pintura).
●
As
amostras foram registradas com intervalos de 15 minutos.
●
Período
dos dados coletados para treino e teste é de janeiro a setembro de 2023.
●
Os
valores ausentes na variável "ciclos", foram interpretados e
substituídos por zero, conforme orientação do stakeholder.
Para a seleção de variáveis, optou-se por remover as três
variáveis do banco de dados após a Análise Exploratória de Dados (do inglês Exploratory
Data Analysis - EDA) (Figura 1) que possuem os valores de menor correlação,
com base na correlação de Pearson. Assim, foram removidas as variáveis caldeira, água demi e tinta. Todas as análises
realizadas neste estudo foram conduzidas com o conjunto de dados contendo sete
variáveis de kWh e uma variável de ciclos.
3.2 METODOLOGIA PROPOSTA
Propõe-se uma arquitetura
de três steps para prever o
consumo energético e maximizar o ciclo de produção em um instante de tempo t+1,
utilizando técnicas de ML, DL e algoritmos meta-heurísticos de otimização. A
abordagem deste trabalho propõe a avaliação de pelo menos três modelos em cada step,
aquele que apresentar o melhor desempenho irá compor a arquitetura. A Figura 1
apresenta a arquitetura que implementa os três steps e seus respectivos
modelos [25].
Os Steps 1 e 2, embora
façam parte de uma sequência lógica, podem ser vistos como duas predições
independentes. Isso significa que, na prática, eles podem ocorrer
simultaneamente ou em qualquer ordem, sem comprometer a eficácia da arquitetura
proposta. Essa flexibilidade permite otimizar o tempo de processamento e
adaptar a abordagem às necessidades específicas de cada aplicação. Os modelos
RF, LSTM, XGBoost e GA utilizados nestes trabalhos foram replicados conforme
estado a arte e os experimentos realizados por Oliveira et al. [24].
3.2.1 Step
1 - Predição do consumo energético
Este step consiste em
prever o consumo de energia em determinado período a partir dos dados
históricos, utilizando técnicas de análise de séries temporais, além dos
modelos implementados por Oliveira et al. [25], utilizou-se o modelo híbrido GRU-LSTM como
nova proposta de implementação tendo como fundamentação os resultados
promissores obtidos em estudos referenciados neste trabalho. A arquitetura do
modelo GRU-LSTM conta com uma camada GRU, uma camada LSTM e duas camadas RNA
Densas, definidas a partir de experimentações e ajustes em busca de melhores
resultados e custo computacional otimizado.
Os modelos são treinados
com os dados do consumo energético de cada processo e têm como alvo t+1,
portanto, o objetivo é estabelecer uma previsão precisa do consumo energético
para o próximo ciclo de produção. Cada amostra do dataset é um vetor de
sete valores de KWh(X) correspondentes aos sete processos do setor de pintura
em um dado tempo t, os quais são as variáveis utilizadas neste estudo. Tanto a
GRU como a LSTM têm como entrada um conjunto de d amostras do dataset,
onde d é o valor do lag.
Assim, se desejamos
utilizar 3 amostras (lag=3) para prever a quarta, temos: como entrada no
modelo 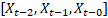 e [
e [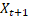 ] como saída. O valor do lag
foi otimizado em função do modelo híbrido GRU-LSTM com auxílio da função
ParameterGrid da biblioteca scikit-learn a fim de buscar valores para o lag que
pudessem gerar os melhores resultados para o modelo híbrido implementado neste step
1 da arquitetura proposta. Na Figura 2 são apresentados os MAEs obtidos
para cada lag em [3, 5, 6, 7, 8, 9, 10, 12, 16, 20, 30, 40, 60]. O lag
igual a 7 apresentou o melhor valor de MAE para o modelo híbrido,
portanto, são 49 valores de KWh distribuídos em 7 vetores utilizados como
entrada tanto na GRU como na LSTM.
] como saída. O valor do lag
foi otimizado em função do modelo híbrido GRU-LSTM com auxílio da função
ParameterGrid da biblioteca scikit-learn a fim de buscar valores para o lag que
pudessem gerar os melhores resultados para o modelo híbrido implementado neste step
1 da arquitetura proposta. Na Figura 2 são apresentados os MAEs obtidos
para cada lag em [3, 5, 6, 7, 8, 9, 10, 12, 16, 20, 30, 40, 60]. O lag
igual a 7 apresentou o melhor valor de MAE para o modelo híbrido,
portanto, são 49 valores de KWh distribuídos em 7 vetores utilizados como
entrada tanto na GRU como na LSTM.
Figura 2 - Variação do erro em função dos lag’s.
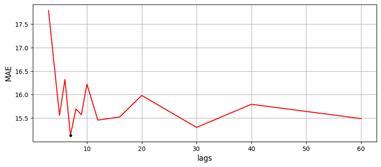
Fonte Autores
Os hiperparâmetros
utilizados no modelo híbrido GRU-LSTM para este experimento estão descritos na
Tabela 1. A utilização de múltiplas rodadas de experimentos, consideram apenas
a variação dos hiperparâmetros e da configuração de divisão do dataset
para treino:teste que é de 80:20, 75:25 e 70:30, sendo esta última a versão
final utilizada no experimento realizado.
3.2.2 Step
2 - Predição Do Ciclo De Produção
No segundo step,
segue-se a arquitetura proposta para os modelos RF, RNA Densa e GXBoost.
Utilizou-se a mesma base de dados do step 1 deste trabalho para
treinamento dos modelos que preveem o ciclo de produção de uma pintura
automotiva. Os hiperparâmetros de cada modelo estão descritos na Tabela 1.
3.2.3 Step
3 - Otimização Utilizando Algoritmos Evolutivos
No último step, são
empregados algoritmos evolutivos GA, PSO e DE para maximizar o ciclo de
produção a partir do consumo energético previsto pelo melhor modelo do step
1. Os otimizadores utilizam como função de aptidão (do inglês fitness) o
melhor modelo do step 2. O espaço de busca dos algoritmos é definido a
partir do vetor de consumo energético previsto pelo melhor modelo do step
1.
Os limites superiores do
espaço de busca são definidos pelo vetor predito no step 1, enquanto os
limites inferiores são definidos por uma redução percentual de 20% (definido
pelas estratégias de negócio) do mesmo vetor.
Cada otimizador inicializa
um conjunto de indivíduos de forma aleatória (entrada do modelo), onde cada
indivíduo representa um vetor de consumo energético e uma possível solução do
problema, cuja aptidão é o número de ciclos de produção. O otimizador que, ao
final de i gerações, apresentar a melhor solução (saída do modelo), será
escolhido como resultado do terceiro step.
Tabela 1 - Hiperparâmetros dos
modelos e otimizadores.
|
Modelo
|
Principais Parâmetros
|
|
RF
|
estimators= 50; min_samples_leaf=6
|
|
XGBoost
|
max_depth=6; learning_rate=0,3
|
|
GRU-LSTM
|
Units=32; loss=mse; optimizer=adam;
epoch=400; batch_size=16
|
|
DL
|
activation (hidden layers) = sigmoid;
activation (output layer)=relu
|
|
GA
|
mutation_probability=0.01; elitism=0.1;
crossover_probability=0.7
|
|
DE
|
crossover_probability=0.7; F=0.6
|
|
PSO
|
w=0.1; 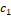 =0.1; =0.1; 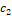 =0.2 =0.2
|
Fonte Autores
Os três otimizadores foram
definidos com população de 50 indivíduos e otimizados em 100 gerações. Outros
parâmetros, específicos de cada otimizador, foram definidos a partir de
diferentes experimentações e são apresentados na Tabela 1.
3.3
AVALIAÇÃO DO DESEMPENHO DOS MODELOS
Para avaliação
de desempenho dos modelos preditores foram utilizadas as seguintes métricas:
Erro Médio Absoluto (do inglês Mean Absolute Error - MAE), Pontuação de
Variância Explicada (do inglês Explained Variance Score - EVS) e Erro
percentual médio absoluto (do inglês Mean Absolute Percentual Error -
MAPE). A métrica MAE é a diferença média absoluta entre os valores reais e os
valores previstos (Equação 12). EVS explica a dispersão dos erros (Equação 13)
e a métrica MAPE mostra o erro (%) em relação aos valores reais (Equação 14).
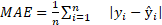 (12)
(12)
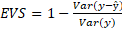 (13)
(13)
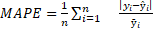 (14)
(14)
Onde n é o
número de amostras, 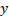 é o valor verdadeiro,
é o valor verdadeiro, 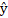 é o valor predito e
é o valor predito e  é a média dos valores
verdadeiros.
é a média dos valores
verdadeiros.
4 RESULTADOS E DISCUSSÃO
Nesta seção são apresentados os resultados dos modelos e
otimizadores de cada step, discussão dos resultados e arquitetura final.
4.1 RESULTADOS DO STEP 1
Neste step, os 4 modelos foram avaliados a partir das
métricas MAPE e EVS.
Tabela 2 - Avaliação dos modelos no
step 1.
|
Modelo
|
MAPE
|
EVS
|
|
RF
|
10,1%
|
0,85
|
|
LSTM
|
8,2%
|
0,91
|
|
XGBoost
|
7,9%
|
0,88
|
|
GRU-LSTM
|
7,8%
|
0,90
|
Fonte Autores
Figura 3 - Previsão da variável ventilação do
GRU-LSTM
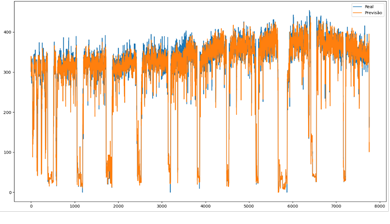
Fonte Autores
Optou-se por utilizar o MAPE para melhor compreensão do erro
dos valores preditos de consumo energético em t+1. A LSTM apresentou os
melhores valores para EVS (0,91) e a GRU-LSTM apresentou o melhor resultado
para o MAPE e o segundo melhor para EVS (0,90). Escolheu-se a GRU-LSTM como
melhor modelo para o step 1, pois o seu MAPE é 0,4% menor e o EVS é apenas
0,01% maior quando comparado com a LSTM, conforme a Tabela 2. A Figura 3 mostra
a previsão do modelo GRU-LSTM para a variável ventilação.
4.2 RESULTADOS DO STEP 2
Para avaliação dos modelos do step 2, o MAE foi preferível pela
possibilidade de observar erro absoluto dos modelos para a quantidade de carros
produzidos, melhorando a análise dos resultados pelos stakeholders envolvidos
no processo. O EVS foi utilizado novamente neste step.
Tabela 3 - Avaliação dos modelos no
step 2
|
Modelo
|
MAE
|
EVS
|
|
RF
|
1,62
|
0,84
|
|
RNA Densa
|
1,59
|
0,85
|
|
XGBoost
|
1,66
|
0,84
|
Fonte Autores
Figura 4 - Predição do ciclo de
produção utilizando o modelo RNA Densa.
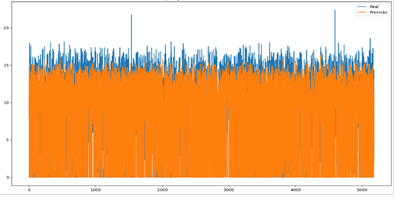
Fonte Autores
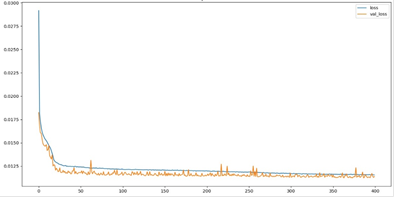
Figura
5 - Curvas de convergência:
modelo RNA Densa.
Fonte Autores
Na Tabela 3, o modelo RNA Densa se destaca como melhor modelo na predição
dos ciclos de produção ao alcançar os melhores resultados para MAE (1,59) e EVS
(0,85). A Figura 4 apresenta a predição de ciclos do modelo RNA Densa e a
Figura 5 mostra a curva de convergência de treino e validação após 400 épocas
de treinamento.
4.3 RESULTADOS DO STEP 3
O step 3 depende dos resultados dos steps anteriores, uma vez que
o melhor modelo do step 1 é responsável por prever o vetor de consumo
energético que define o espaço de busca e o melhor modelo do step 2 é definido
como função fitness dos 3 otimizadores. Portanto, no step 3, a
arquitetura já se encontra definida com a GRU-LSTM para o step 1 e RNA Densa.
para o step 2.
A previsão do modelo produzido no step 1 resultou no vetor de
consumo energético, cujo consumo total foi de 1818,0 KWh e ciclo produtivo
igual a 5,58 - ciclo previsto no step 2, tomando como vetor de entrada o vetor
predito no step 1.
O vetor predito foi definido como o limite superior do espaço de busca,
enquanto o limite inferior foi definido aplicando uma redução de 20% em relação
ao limite superior. Todas as possíveis soluções de cada otimizador percorreram
um espaço de busca que reflete de 80% a 100% do consumo máximo previsto no step
1.
Tabela 4 - Desempenho dos
otimizadores
|
Otimizador
|
Total kWh
|
Redução kWh
|
Ciclo (fitness)
|
|
GA
|
1527,01
|
290,99
|
10,58
|
|
DE
|
1517,15
|
300,80
|
10,66
|
|
PSO
|
1668,88
|
149,12
|
12,70
|
Fonte Autores
A Tabela 4 mostra os resultados da melhor solução de cada otimizador após
100 gerações. O DE foi o que apresentou o melhor resultado em otimização do
vetor energético de 1818,0 KWh (step 1) para 1517,15 kwh, reduzindo consumo
em 16,5%. Para ciclo de produção, a melhor otimização é realizada pelo PSO,
maximizando o valor do ciclo predito no step 2 (5,58 ciclos) para 12,70 ciclos,
resultando em otimização de 127%.
Os valores encontrados
ressaltam a importância de selecionar o algoritmo de otimização mais adequado para
o objetivo de negócio na organização estudada. Apesar do PSO apresentar melhor otimização
de ciclos de produção, a integração do DE na arquitetura final do step 3
representa uma decisão estratégica, a partir de alinhamentos com o stakeholder,
baseada na busca por eficiência energética. Portanto, a arquitetura final foi
composta pelos modelos GRU-LSTM, DL e DE nos steps 1, 2 e 3,
respectivamente.
4.4 DISCUSSÃO
A arquitetura final é composta pelos modelos GRU-LSTM,
RNA Densa e DE nos steps 1, 2 e 3, respectivamente, conforme o fluxograma de
execução das atividades realizadas e sua consolidação proposta como objetivo
para o presente estudo, observado no campo "Arquitetura Final" da
Figura 1. Essa estrutura é resultado de análises e de modelagens de ML e DL, com
cada etapa sendo relevante para os resultados.
Os resultados refletem não apenas os métodos
convencionais de experimentação, mas também as estratégias de negócios
definidas pelos stakeholders, que vão desde o processamento dos dados até a
fase final da arquitetura de steps. Os resultados obtidos nos steps 1, 2 e 3
demonstram melhorias em relação a trabalhos anteriores [25] que foram alcançadas tanto pela
introdução de novos modelos e otimizadores, como também pela mudança na análise
dados na fase de pré-processamento, que implicaram na remoção das variáveis com
baixa correlação de Pearson.
Como neste estudo, os
trabalhos de Hong et al. [26], Zafar
et al. [20] e Kervanci et al. [27], os modelos híbridos GRU-LSTM propostos
por eles se destacam em relação aos demais modelos analisados. Esse ganho se
deve ao fato de o modelo híbrido conseguir capturar relações temporais
complexas e de curto e longo prazo. Embora os modelos RF e XGBoost não
possuírem uma arquitetura projetada para capturar explicitamente relações temporais
como as RNNs, são capazes de obter resultados próximos à LSTM-GRU e DL devido
suas arquiteturas ensemble e flexibilidade em lidar com diferentes padrões de
dados.
5 CONCLUSÃO
A nova abordagem composta
pela arquitetura de 3 steps se mostrou promissora na previsão e otimização do
consumo energético em oficinas de pintura automotiva. A arquitetura final foi
capaz de prever e minimizar o consumo energético em até 16% e maximizar o ciclo
produtivo a partir dos modelos GRU-LSTM, DL e DE. Os resultados evidenciaram o
potencial significativo dessa abordagem integrada de técnicas de ML, DL,
abordagens híbridas e algoritmos evolutivos para promover uma gestão mais
inteligente e sustentável do consumo energético em ambientes industriais, como
as oficinas de pintura automotiva.
Para trabalhos futuros, é
possível explorar outras oportunidades não abordadas neste estudo. Isso pode
incluir a incorporação de outros modelos nos steps 1 e 2 da arquitetura e a
exploração de outros modelos híbridos, visando uma análise mais abrangente e
precisa dos dados. Além disso, a consideração de diferentes restrições no
espaço de busca, alinhadas com as estratégias ou regras de negócio e validação
cruzada na base de dados podem levar a soluções ainda mais otimizadas. A interpretabilidade
e a explicabilidade de datasets e modelos podem ser considerados como
novos testes para compreensão dos resultados.
REFERÊNCIAS
[1] OKTAVIANDRI, M.; SAFIEE, A. S. B. Modelling
Electrical Energy Consumption in Automotive Paint Shop. In: IOP Conference
Series: Materials Science and Engineering. IOP Publishing, 2018. p. 012060.
[2] GIAMPIERI, A. et al. A review of the
current automotive manufacturing practice from an energy perspective. Applied
Energy, v. 261, p. 114074, 2020.
[3] ĐAKOVIĆ, D. et al. Review of Energy-Related
Machine Learning Applications in Drying Processes. Energies, v. 17, n. 1, p.
224, 2023.
[4] Mandal, S., Anderson, T.A., Turek, J.S.,
Gottschlich, J., Zhou, S., Muzahid, A.: Learning fitness functions for machine
programming (2021)
[5] WANG, Z. et al. Random Forest based hourly
building energy prediction. Energy and Buildings, v. 171, p. 11-25, 2018.
[6] FATAHI, R. et al. Modeling of energy
consumption factors for an industrial cement vertical roller mill by SHAP-XGBoost:
a" conscious lab" approach. Scientific Reports, v. 12, n. 1, p. 7543,
2022.
[7] JIANG, P. et al. Energy consumption
prediction and optimization of industrial robots based on LSTM. Journal of
Manufacturing Systems, v. 70, p. 137-148, 2023.
[8] BASHIR, T. et al. Short term electricity
load forecasting using hybrid prophet-LSTM model optimized by BPNN. Energy
reports, v. 8, p. 1678-1686, 2022.
[9] LU, Y. et al. Prophet-EEMD-LSTM based
method for predicting energy consumption in the paint workshop. Applied Soft
Computing, v. 143, p. 110447, 2023.
[10] MA, S.; JIANG, Z.; LIU, W. Modeling
drying-energy consumption in automotive painting line based on ANN and MLR for
real-time prediction. International Journal of Precision Engineering and
Manufacturing-Green Technology, v. 6, p. 241-254, 2019.
[11] SZÁSZ, L.; CSÍKI, O.; RÁCZ, B.
Sustainability management in the global automotive industry: A theoretical
model and survey study. International Journal of Production Economics, v. 235,
p. 108085, 2021.
[12] LUKIN, E.; KRAJNOVIĆ, A.; BOSNA, J.
Sustainability strategies and achieving SDGs: A comparative analysis of leading
companies in the automotive industry. Sustainability, v. 14, n. 7, p. 4000,
2022.
[13]
CAVALCANTE, E. S. et al.
Automotive painting process: Minimizing energy consumption by using adjusted
convective heat transfer coefficients. Progress in Organic Coatings, v. 140, p.
105479, 2020.
[14]
HOVGARD, M.; LENNARTSON,
B.; BENGTSSON, K. Energy-Optimal Timing of Stochastic Robot Stations in
Automotive Production Lines. In: 2022 IEEE 27th International Conference on
Emerging Technologies and Factory Automation (ETFA). IEEE, 2022. p. 1-7.
[15] ILBEIGI, M.; GHOMEISHI, M.;
DEHGHANBANADAKI, Ali. Prediction and optimization of energy consumption in an
office building using artificial neural network and a genetic algorithm.
Sustainable Cities and Society, v. 61, p. 102325, 2020.
[16]
NARCISO, D. A.; MARTINS, F.
G. Application of machine learning tools for energy efficiency in industry: A
review. Energy Reports, v. 6, p. 1181-1199, 2020.
[17] YANG, S.; YU, X.; ZHOU, Y. Lstm and gru neural network
performance comparison study: Taking yelp review dataset as an example. In:
2020 International workshop on electronic communication and artificial
intelligence (IWECAI). IEEE, 2020. p. 98-101.
[18] CAHUANTZI, R.; CHEN, X.; GÜTTEL, S. A
comparison of LSTM and GRU networks for learning symbolic sequences. In:
Science and Information Conference. Cham: Springer Nature Switzerland, 2023. p.
771-785.
[19] HONG, J. et al. Multi-forword-step state of charge
prediction for real-world electric vehicles battery systems using a novel
LSTM-GRU hybrid neural network. eTransportation, p. 100322, 2024.
[20] ZAFAR, N. et al. Applying hybrid LSTM-GRU
model based on heterogeneous data sources for traffic speed prediction in urban
areas. Sensors, v. 22, n. 9, p. 3348, 2022.
[21] HOCHREITER, S.; SCHMIDHUBER, J. Long
short-term memory. Neural computation, v. 9, n. 8, p. 1735-1780, 1997.
[22]
ABDEL-BASSET, M.;
ABDEL-FATAH, L.; SANGAIAH, A. K. Metaheuristic algorithms: A comprehensive
review. Computational intelligence for multimedia big data on the cloud with
engineering applications, p. 185-231, 2018.
[23] WANG, D.; TAN, D.; LIU, L. Particle swarm
optimization algorithm: an overview. Soft computing, v. 22, p. 387-408, 2018.
[24] OPARA, K. R.; ARABAS, J. Differential Evolution: A
survey of theoretical analyses. Swarm and evolutionary computation, v. 44, p.
546-558, 2019.
[25] DE OLIVEIRA, R. B. et al. Análise de
Consumo de Energia Elétrica de Equipamentos em Oficina de Pintura Automotiva.
Revista de Engenharia e Pesquisa Aplicada, v. 9, n. 1, p. 69-78, 2024.
[26] HONG, Jichao et al. Multi-forword-step state of charge
prediction for real-world electric vehicles battery systems using a novel
LSTM-GRU hybrid neural network. eTransportation, p. 100322, 2024.
[27] KERVANCI, I. S.; AKAY, M. F.; ÖZCEYLAN, E. Bitcoin
price prediction using LSTM, GRU and hybrid LSTM-GRU with bayesian
optimization, random search, and grid search for the next days. Journal
Industrial and Management Optimization, v. 20, n. 2, p. 570-588, 2024.