1 INTRODUÇÃO
Ao longo das últimas
décadas tem-se assistido o auge da intervenção humana sobre o planeta,
principalmente após o surgimento das indústrias siderúrgicas, produtos químicos
e a queima de combustíveis fósseis. Essas intervenções não foram acompanhadas
de análises que possibilitassem avaliar o impacto causado ao meio ambiente ou
os prováveis danos à saúde. Portanto, há alguns anos é possível observar as
consequências prejudiciais causadas por este processo desordenado. O objetivo
atual possui como finalidade adquirir conhecimento sobre os resíduos
resultantes de modo a evitar os efeitos prejudiciais ao ambiente e
consequentemente, aos seus habitantes.
O ar
apresenta-se como elemento com maior prejuízo devido à intervenção humana no
ambiente. Este fato ocorre principalmente nos grandes centros urbanos, que
possuem como principais fontes poluidoras a crescente presença de automóveis
juntamente com a indústria [1].
A poluição
atmosférica refere-se à contaminação do ar pela introdução de substâncias
conhecidas por poluentes atmosféricos, os mesmos podem se apresentar em forma
de gases e partículas provenientes de fontes naturais (vulcões, neblinas) ou
produzidas pela atividade humana (queima de carvão, indústrias, escapamento de
veículos). A poluição atmosférica traz prejuízos não somente à saúde e à
qualidade de vida das pessoas, mas também acarretam maiores gastos do Estado,
decorrentes do aumento do número de atendimentos e internações hospitalares,
além do uso de medicamentos, custos esses que poderiam ser evitados com a melhoria
da qualidade do ar nos centros urbanos. Existe, igualmente, o prejuízo causado
à qualidade dos materiais (corrosão), do solo e das águas (chuvas ácidas) além
de afetar a visibilidade. Ademais, a poluição do ar é considerada pela OMS
(Organização Mundial da Saúde) o maior risco ambiental para a saúde no mundo, e
a estimativa é a de que todos os anos cerca de 8 (oito) milhões de pessoas
morrem em decorrência desta exposição [2,3].
Entre os
poluentes atmosféricos que mais acarretam em preocupações à saúde pública,
estão incluídos: o material particulado (PM), o monóxido de carbono (CO), o
ozônio (O3) e o dióxido de nitrogênio (NO2) [3]. Dentre os poluentes citados, aquele que causa um
maior impacto negativo à saúde humana é o PM. Este, normalmente é medido pela
concentração de partículas finas suspensas no ar com diâmetro menor que 10,0
micrômetros (PM10) ou 2,5 micrômetros (PM2,5). Essas partículas são capazes de
penetrar profundamente no sistema respiratório e causar danos à saúde [4,5].
A maior
parcela do material particulado urbano é originada pela queima de combustível,
por processos industriais, pela névoa salina e ressuspensão do solo. Sua
dispersão ocorre em função das condições meteorológicas e da topografia local.
Enquanto que os efeitos adversos à saúde humana dependem de suas propriedades
físico-químicas, diâmetro médio e tempo de exposição. O principal efeito é
irritação no sistema respiratório, devido principalmente, ao PM10. Este
material particulado transforma quimicamente os poluentes iniciais em
substâncias mais nocivas, e atua como vetor de microrganismos, substâncias
orgânicas e cancerígenas [6].
Estimativas
das concentrações de PM10 permitem avaliar os padrões de qualidade do ar e
possíveis ações de proteção à população, particularmente em eventos extremos. O
uso da modelagem matemática computacional fornece condições de quantificar as
tendências temporais de cada poluente atmosférico e chegar a uma estimativa dos
potenciais efeitos à saúde com relação a poluição do ar. Portanto, o estudo da
qualidade do ar, assim como a simulação para previsão acurada de seus
principais poluentes, se torna de grande valia para fins de prevenção e
controle, sendo a principal importância deste tema creditada à relação
existente entre as altas concentrações de poluentes, e os efeitos adversos à
saúde humana [4, 7, 8].
Estudos
prévios utilizaram modelos estatísticos e métodos de inteligência computacional
para analisar e prever as concentrações de material particulado e outros
poluentes presentes no ar. Alguns trabalhos estudaram abordagens variadas, como
a regressão linear, não linear e métodos de aprendizado de máquinas para
avaliar qual deles fornecem uma previsão mais acurada da concentração do PM10
em região urbana [8].
Arquiteturas de rede neural do tipo MLP, com otimização de parâmetros por meio
de algoritmo genético e ajuste de fase foi desenvolvida e testada na previsão
tanto do PM10 quanto do PM2.5 [9,4]. Estudos que comparam a capacidade de previsão do modelo de
regressão linear múltipla com outros modelos estatísticos, como o
autorregressivo e de Box-Jenkis, para séries temporais de poluentes
atmosféricos, também já foi trabalhado [10]. Assim como análises envolvendo aplicação de máquinas
desorganizadas (Extreme Learning Machines - ELM) e rede neural com
estado de eco (Echo State Networks - ESN) na previsão do PM [11].
Os objetivos
deste trabalho foram de estimar a concentração do poluente atmosférico PM10 em
função das condições meteorológicas utilizando modelos estatísticos de
regressão linear e avaliar a influência dos parâmetros meteorológicos na
concentração deste mesmo poluente na Região Metropolitana do Recife (RMR) - PE.
2
MATERIAIS E MÉTODOS
2.1
PM10 e Variáveis
Meteorológicas
Foram obtidas
concentrações de material particulado com diâmetro inferior a 10µm (PM10,
µg/m³), presentes no ar, para o período de 17/07/2015 a 09/04/2017, através da
Agência Estadual de Meio Ambiente de Pernambuco (CPRH). Para o mesmo período do
poluente atmosférico, foram obtidas as medidas meteorológicas: velocidade do
vento (WS, m/s), umidade relativa do ar (RH, %) e temperatura (AT, C°). Todas
as medições foram feitas em intervalos de 1h e foram extraídas da estação de
monitoramento do ar instalada na Escola de Referência em Ensino Médio Frei
Otto, em Nossa Senhora do Ó, localizada no município de Ipojuca, Estado de
Pernambuco. O sistema da estação de monitoramento capta as informações em tempo
real por meio de sensores e envia todo o conteúdo pela internet para a sede da
agência na cidade do Recife-PE.
A Figura 1
mostra a localização aproximada do ponto de coleta (Estação Gaibú, acima a
direita) cujas coordenadas geográficas são: 8º 19’ 44,37’’ (S) e 34º 57’
22,66’’ (O). Na parte inferior esquerda, com o círculo amarelo, se encontra a
Refinaria Abreu e Lima (RNEST) na rodovia PE 60.
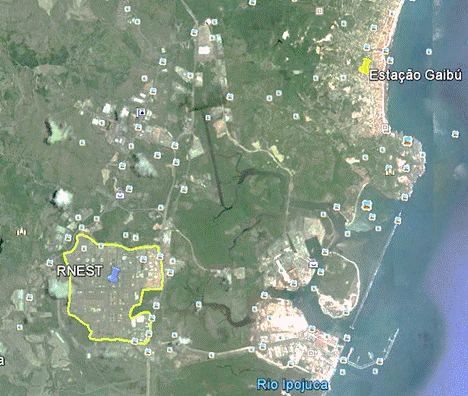
Figura 1: Localização aproximada da Estação de Qualidade do Ar.
Fonte: JCTM, Monitoramento da Qualidade do Ar, Estação RNEST
– GAIBU, 26/02/2017 a 25/03/2017.
A Tabela-1
apresenta a estatística descritiva para as séries de dados referentes ao PM10 e
parâmetros meteorológicos usados neste estudo.
Tabela 1: Estatística dos dados
utilizados.
|
Parâmetro
|
Média
|
Desvio
Padrão
|
Coeficiente de
Variação
|
|
PM10 (µg/m³)
|
35,802
|
22,998
|
0,648
|
|
WS (m/s)
|
3,422
|
0,957
|
0,290
|
|
RH (%)
|
73,507
|
9,139
|
0,121
|
|
AT (ºC)
|
27,762
|
2,110
|
0,072
|
Fonte: Autor.
2.2
Modelos de Regressão Linear
A análise de
regressão é uma técnica estatística para modelar e investigar a relação entre
duas ou mais variáveis, muitos problemas em engenharia e ciências envolvem
explorar essa relação [12].
Esse tipo de relacionamento é representado por um modelo matemático, que, na
verdade, se trata de uma equação que associa a variável dependente (que se
deseja prever) às variáveis independentes (preditoras). Sendo assim, análise de
regressão tem por objetivo desvendar o comportamento entre uma variável
dependente e as consideradas independentes.
Para fins de
aplicação dos modelos de regressão linear, foram desenvolvidos dois modelos em
linguagem C, denominados de RLS (Regressão Linear Simples) e RLM (Regressão
Linear Múltipla). Estes, ao receberem as séries de dados apropriadas, se
encarregam de efetuar as operações de regressão. Foi utilizado o ambiente de
desenvolvimento integrado (IDE) de código aberto Code::Blocks
(www.codeblocks.org/) versão 16.01, para codificar, compilar e executar os
programas. Ambos foram implementados contendo um algoritmo de busca exaustiva
em sua estrutura com a finalidade de gerar todas as possíveis combinações de
variáveis independentes e verificar com qual delas obtêm-se as melhores
previsões para os poluentes considerados. A variável dependente é representada
por PM10, as variáveis independentes são: WS-i, RH-i e AT-i, além de PM10-i (em
que “-i” representa a série de dados defasada em i hora(s)).
O modelo RLS
explora a relação entre duas variáveis, para este caso, considera-se uma única
variável independente (preditora, x) e uma única variável dependente (ou
variável de resposta, Y) a formulação do modelo de regressão linear simples é
descrita a seguir:
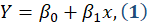
em queβ0e β1são coeficientes de regressão
desconhecidos a princípio. Para obter os coeficientes, o modelo RLS utiliza
estimativa de mínimos quadrados, estimando a interseção (β0) e a inclinação da reta (β1) por:
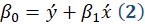
e
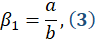
em que:
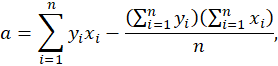
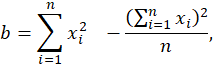
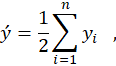
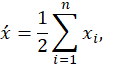
e nrepresenta o número de pares de
observação (x1, y1), (x2, y2),
..., (xn, yn).
Aplicações
mais interessantes da análise de regressão geralmente exigem o uso de mais de
uma variável regressora, pois muitas vezes, uma única variável não é capaz de
explicar tudo a respeito da variável resposta. Para tanto, o modelo RLM analisa
a relação entre duas ou mais variáveis, caracterizando assim modelos de
regressão linear múltipla. Nesta abordagem, a variável resposta Y pode estar
relacionada com duas ou mais variáveis independentes, sendo sua formulação
descrita a seguir:
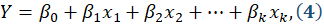
em que, β0 representa a interseção do plano,
todos os parâmetros
βj, j=1, 2, 3, ..., k, são chamados de coeficientes de
regressão e a estimativa destes parâmetros pode ser feita através do método dos
mínimos quadrados. Agora, as observações da série são descritas da seguinte
forma, n continua representando o número de observações e suponha que n
> k, seja xij a i-ésima observação, logo as
observações são:
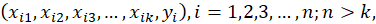
em que cada
uma das observações satisfaz a equação (4) [12].
O modelo RLM
realiza a estimativa dos coeficientes de regressão através da resolução do
sistema de equações normais de mínimos quadrados (5).
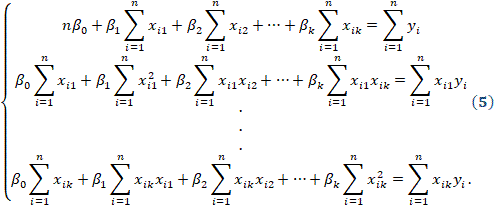
A resolução do
sistema é efetuada utilizando-se o algoritmo de eliminação gaussiana (ou método
de escalonamento), que simplifica um sistema de várias incógnitas e o resolve
automaticamente, fornecendo ao usuário os k coeficientes de regressão de
cada equação, para cada combinação de variáveis.
2.3 Métricas de Desempenho
Para medir o
desempenho de cada equação de regressão ao problema proposto, os dois modelos
foram desenvolvidos para trabalhar com 2 métricas principais, são elas: erro
quadrado médio (mean square error - MSE) e o índice de concordância (index
agreement – IA). Além do Coeficiente de Determinação (R²) e o Coeficiente de Correlação (R).
O R² varia entre 0 e 1, indicando em
percentagem o quanto o modelo consegue explicar a variação dos valores observados
para o PM10. O R varia entre -1 e 1, servindo para medir o grau com que duas
variáveis estão correlacionadas e a direção dessa correlação (se positiva ou
negativa). É importante salientar que, o índice de concordância, é utilizado
para indicar o nível de concordância entre a equação de regressão e a variável
prevista, sendo a principal métrica adotada neste trabalho por conta de sua
constante utilização em outros estudos sobre o tema.
O MSE é
frequentemente utilizado na previsão de séries temporais, sua principal função
é indicar se a previsão feita pelo modelo está superestimada ou subestimada.
No entanto,
não se pode tomar conclusões apenas com base no MSE [13, 14]. Quanto mais próximo de zero, melhor
os resultados de previsão fornecidos pelo modelo testado.
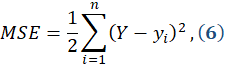
em que 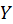 representa o valor previsto pelo
modelo e
representa o valor previsto pelo
modelo e 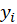 o valor observado (real) na série da
variável resposta.
o valor observado (real) na série da
variável resposta.
O IA foi
desenvolvido como uma medida padronizada do grau de erro de previsão do modelo
e varia entre 0 e 1. Um valor de 1 para o IA indica uma correspondência
(concordância) perfeita entre o modelo e a variável prevista, e 0 indica nenhum
tipo de concordância entre eles [15].
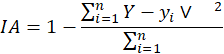
em que 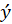 representa a média de todas as
observações da variável de saída.
representa a média de todas as
observações da variável de saída.
No
desenvolvimento dos modelos de regressão foi levado em consideração uma
defasagem de até 6 (seis) horas para as variáveis independentes. As equações de
regressão trabalhadas utilizam até 3 (três) elementos meteorológicos e sempre
no mínimo uma série de dados defasadas do poluente como variável independente.
Sendo assim, contabiliza-se 4 (quatro elementos) x 6 (defasagem de seis horas
para cada variável) = 24 (vinte e quatro) variáveis no total a serem
consideradas no desenvolvimento das equações de regressão.
Usando o
conceito matemático de combinação linear, é possível calcular que foram geradas
15.600.443 (mais de 15 milhões de combinações) equações de regressão no total,
sendo que, cada uma delas fornece um resultado diferente da previsão, melhor ou
pior, por isso a importância da implementação de um algoritmo de busca
exaustiva que teste cada uma delas e indique com qual obteve-se a melhor
métrica IA e, consequentemente as melhores métricas.
Na fase de treino, foram utilizados os
dados de concentração do PM a partir das 0h do dia 17/07/2015 até as 22h do dia
08/02/2017, totalizando 13.751 horas. Os dados de 23h do dia 08/02/2017 até as
23h do dia 09/04/2017 (num total de 1.441 horas) foram direcionadas para testar
cada uma das equações obtidas na fase de treino.
3 RESULTADOS E DISCUSSÃO
Foram analisados os resultados fornecidos pelos dois
modelos (RLS e RLM). Primeiramente, os resultados obtidos quando se utiliza o
PM10 para prever a si mesmo sem levar em consideração os parâmetros
meteorológicos, a posteriori, os resultados referentes às equações que levam em
consideração, além do próprio PM10 defasado, também os parâmetros
meteorológicos. Foi dada especial atenção as equações que obtiveram o melhor
desempenho na previsão da concentração do poluente em estudo.
3.1 Modelo de Previsão sem Parâmetros
Meteorológicos
A Tabela-2
apresenta o Coeficiente de Determinação (R²), o Coeficiente de Correlação (R), além das métricas já discutidas,
entre o PM10 e os dois melhores modelos de previsão obtidos. É analisado
inicialmente o modelo que não leva em consideração as variáveis meteorológicas
(1). Utilizando o PM10 defasado em até 6 horas como variável independente e
usando todas as combinações possíveis destas, foram obtidas 63 equações de
regressão.
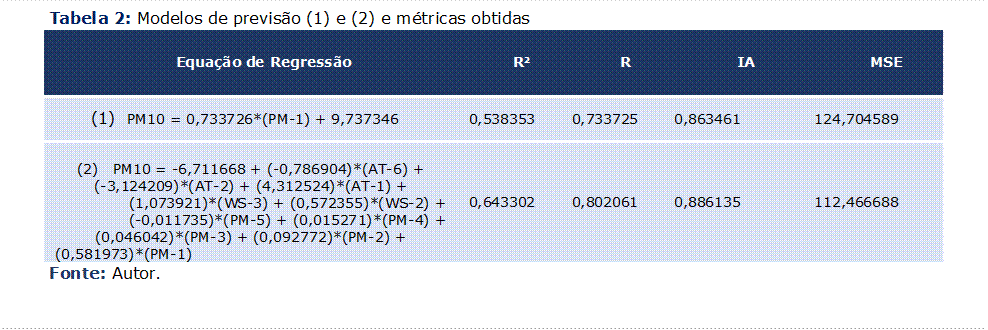
Observa-se
que, a relação linear entre o PM10 e sua concentração na hora anterior
apresenta um R² = 0,54, revelando que as concentrações do PM10 podem ser influenciadas
fortemente por seus valores registrados em horas anteriores. O IA fornecido
pela equação foi próximo a 1, indicando uma boa correspondência (concordância)
entre o modelo 1 e a variável PM10, o MSE é de aproximadamente 124,79, o menor
dentre as demais, indicando que esta equação é a que apresenta uma melhor
qualidade em suas previsões, não superestimando ou subestimando tanto quanto as
outras em seus resultados, demonstrando então a importância de se utilizar o
valor da concentração do poluente na hora anterior como variável de entrada
para fins de previsão.
Ainda,
corroborando com os resultados obtidos, observa-se no modelo 1 que o
coeficiente de correlação (R) apresentou um valor de 0,73, indicando uma
correlação forte e positiva entre a concentração do PM10 na hora anterior e a
atual, confirmando que uma equação de regressão simples pode fornecer
resultados razoáveis levando-se em conta que a concentração do material
particulado está sendo estimada com base apenas na concentração observada na hora
anterior.
3.2 Modelo de Previsão com Parâmetros
Meteorológicos
É de
particular interesse o estudo da influência das condições climáticas sobre o
nível de poluição presente no ar. Os parâmetros meteorológicos, por si só, não
oferecem resultados suficientemente aceitáveis na estimativa do PM10, no
entanto, fisicamente, é perceptível que a concentração do poluente sofre
influência da ação do vento, humidade relativa do ar e temperatura. Portanto,
na composição de modelos de regressão, é importante considerar também as
variáveis climáticas como dado de entrada da equação.
Foram geradas e testadas
15.600.380 (além das já citadas no tópico 3.1) equações de regressão múltipla,
sendo essas resultantes das combinações obtidas pela defasagem de até 6 horas
das variáveis WS, RH, AT e do próprio PM10. A Tabela-2 fornece também o modelo
2, no qual a melhor equação de regressão que leva em consideração as variáveis
meteorológicas na previsão do PM10 é representada.
Dentre as variáveis
atmosféricas consideradas, a umidade relativa foi a que apresentou, em módulo,
a maior correlação com o PM10 (R = -0,54), no entanto, de maneira inversa,
quando esta aumenta, a concentração do poluente tende a diminuir. Mas, apesar
deste resultado, destaca-se a ausência do parâmetro meteorológico RH que não
participa como variável de entrada do modelo de regressão 2, na verdade o que
se pôde observar foi que, ao se utilizar o parâmetro RH como variável
explicativa, as equações seguem a tendência de diminuir seu respectivo IA.
Neste ponto, é importante ressaltar que, em geral, quando o tempo está mais
seco, ou seja, quando a umidade relativa do ar diminui (no inverno, por
exemplo), tende a ocorrer um aumento das crises devido a doenças respiratórias
que, por sua vez, estão fortemente relacionadas com a elevação da concentração
do material particulado e de outros poluentes presentes na atmosfera das
grandes cidades.
Quando comparados os dois
modelos, uma significativa melhora é percebida no modelo 2, principalmente
devido a adição dos parâmetros meteorológicos junto com PM10 em horas
anteriores como variável de entrada. Ainda, ocorreu uma diminuição do MSE,
demonstrando que, utilizando esta abordagem, se torna possível realizar
previsões ainda melhores.
Também, ao comparar os
coeficientes de correlação, percebe-se que ocorreu um aumento do potencial
explicativo com o uso da equação 2, comprovando que existe um alto grau de
relacionamento linear entre o conjunto de variáveis climáticas consideradas no
modelo e o PM10, o que de imediato demonstra a vantagem de se utilizar os
parâmetros meteorológicos na previsão do poluente e comprova o relacionamento
físico existente entre eles. O coeficiente de determinação também é maior, o
que o classifica como um modelo que explica melhor a variação do PM10.
A Figura-2 apresenta um
gráfico que representa a concentração real do PM10 (linha preta sólida) e as
estimativas feitas pelas equações de regressão 1 (pontilhado) e 2 (linha
cinza), para os dias 10 e 11/02/2017.
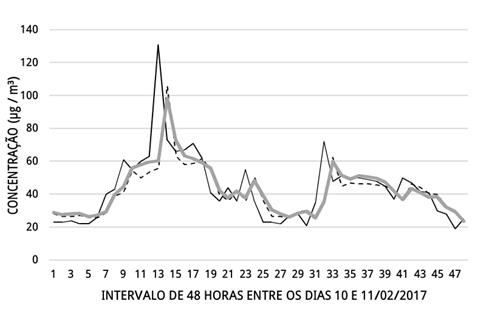
Figura 2: Sobreposição das concentrações do PM10 (em µg/m³) real
e previsto.
Ambas as equações
forneceram bons resultados na maior parte das horas analisadas, no entanto, o
gráfico da equação de regressão 2 demonstrou uma aderência maior aos dados de
concentração real para algumas horas do dia. Este comportamento ficou
evidenciado ao longo do período de tempo considerado.
Por tanto, para as
variáveis trabalhadas e a região em estudo, considerou-se que o modelo 2 obteve
um melhor desempenho. No entanto, vale mencionar que, a modelagem 2
inevitavelmente requer uma maior quantidade de dados a serem processados pelo
computador em uso, isto significando que, apesar desta fornecer melhores
previsões, a mesma apresenta uma complexidade computacional notadamente maior
quando na busca do modelo regressor que melhor se ajuste a saída desejada,
resultando em um tempo mais elevado de processamento.
Para fins de comparação,
considerando o tamanho da série histórica trabalhada, o modelo 1 conclui todas
as suas combinações em no máximo alguns minutos, enquanto que a modelagem 2
exige alguns poucos dias de busca intermitente a fim de fornecer todos os
resultados. Porém, este custo é relativo apenas a fase de busca e, uma vez que
os resultados ideais são apresentados, é possível adotá-los e se ocupar em
trabalhar apenas com as variáveis que levaram a estes.
4 CONCLUSÕES
Apesar da simplicidade do
modelo Estatístico de Regressão Linear frente aos métodos mais sofisticados de
inteligência computacional para previsões de séries temporais, é possível
perceber que ele é capaz de fornecer bons resultados, sendo que a
confiabilidade destes é altamente dependente da qualidade dos dados disponíveis
e das características físicas das variáveis em estudo. O uso das variáveis
meteorológicas temperatura e velocidade do vento, acrescentadas a equação de
regressão 2, permite uma melhoria na estimativa da concentração do poluente
PM10, isto pode ser evidenciado através das métricas consideradas e acontece
porque existe uma interação real ocorrendo entre as partículas de PM10 que
pairam no ar atmosférico e as recorrentes mudanças climatológicas da região
metropolitana do Recife (alterações na velocidade dos ventos, variação de
temperatura, etc.). Dentre os três parâmetros atmosféricos analisados, a
umidade relativa do ar é o que está mais correlacionado com a concentração do
poluente, seu aumento, porém, não contribui para a elevação da concentração do
PM10. Assim, temperaturas altas e ventos mais intensos contribuem para um clima
mais seco que, aliado a presença do material particulado, aumenta a incidência
de doenças tornando mais grave o quadro dos indivíduos mais vulneráveis a
problemas cardiorrespiratórios nas grandes cidades.
AGRADECIMENTOS
A Agência Estadual de Meio Ambiente (CPRH)
pelo fornecimento dos dados necessários. Ao Departamento de Pós-graduação em Engenharia
de Sistemas (PPGES) da Escola Politécnica da Universidade de Pernambuco
(POLI-UPE), que permitiu as simulações matemáticas em seu laboratório. A
Coordenação Setorial de Pós-graduação e Pesquisa da POLI-UPE pela concessão de
bolsa de incentivo à pesquisa.
REFERÊNCIAS
[1] BRAGA, A. et al. Poluição atmosférica e saúde humana. REVISTA
USP, n. 51, p. 58-71, 2001.
[2] QUALIDADE DO AR. In: Ministério do Meio
Ambiente. Disponível em: http://www.mma.gov.
br/cidadessustentaveis/qualidade-do-ar.
Acesso em: 10 jul. 2017.
[3] JASAREVIC, T.; LINDMEIER, C. World Health Assembly closes, passing
resolutions on air pollution and epilepsy. In: World Health
Organization Media Centre, News release. 26 maio 2015. Disponível em: http://www.who.int/mediacentre/news/releases/2015/wha-26-may-2015/en/.
Acesso em: 26 jul. 2017.
[4] MATTOS NETO, P. S. G. de et al. Hybrid intelligent system for air quality
forecasting using phase adjustment. Engineering Applications of Artificial
Intelligence: The International Journal of intelligent Real-Time Automation.
v. 32, p. 185 - 191, jun. 2014.
[5] The
International Bank for Reconstruction and Development / The World Bank. MDGs
and the Environment: Agenda for Inclusive and Sustainable Development, Global
Monitoring Report. Washington DC, 2008.
Technical Report.
[6] LYRA, G. B.; ODA-SOUZA, M.; VIOLA, D. N. Modelos
Lineares aplicados à estimativa da concentração do material particulado (PM10)
na cidade do Rio de Janeiro, RJ. Revista Brasileira de Meteorologia, v.
26, n. 3, p. 392 - 400, 2011.
[7] ZHANG, Ping et al. Temporal and Spatial Simulation of Atmospheric Pollutant PM2.5
Changes and Risk Assessment of Population Exposure to Pollution Using
Optimization Algorithms of the Back Propagation-Artificial Neural Network Model
and GIS. International Journal of Environmental Research and Public Health,
v. 12, n. 10, p. 12171 - 12195, 2015.
[8] SAYEGH, A.; MUNIR, S.; HABEEBULLAH, T. M. Comparing the
Performance of Statistical Models for Predicting PM10 Concentrations. International
journal of Aerosol and Air Quality Research, n. 14, p. 653-665, 2014.
[9] GRIVAS, G.; CHALOULAKOU, A. Artificial neural network models for
prediction of PM10 hourly concentrations, in the Greater Area of Athens,
Greece. Atmospheric Environment, v. 40, p. 1216-1229, 2006.
[10] SAWARAGI, Y. et al. Statistical Prediction of Air Pollution Le-vels
Using Non-Physical Models. Automatica, v. 15,
n. 4 p 441-451, 1979. DOI: https://doi.org/10.1016/0005-1098(79)90018-9.
[11] TADANO, Y.
S. et al. Forecasting
Particulate Matter Concentrations: Use of Unorganized Machines, International
Journal of Advanced Engineering Research and Science, v. 4, p 188-191, Apr.
2017.
[12] MONTGOMERY, D; RUNGER, G. Applied statistics and probability
for engineers. 3. ed. Arizona State University: Wiley, 2003.
[13] MATTOS NETO, P.S.G. de et al. An intelligent perturbative approach
for the time series forecasting problem. In: IEEE WORLD CONGRESS ON
COMPUTATIONAL INTELLIGENCE, 2010, Barcelona. Proceedings… Barcelona: IEEE, 2010. p.1-8.
[14] SOUZA, S. I. V.
et al. Multiple linear regression and artificial neural networks based on
principal components to predict ozone concentrations, Environmental
Modelling & Software, v. 22, p. 97 – 103, 2007.
[15] WILLMOTT, C. J. On the validation
of models. Physical Geography, v. 2, p 184-194, 1981.
orcid.org/0000-0002-9329-6220
orcid.org/0000-0003-3129-0453